types of graphical representation

Number System and Arithmetic
Probability
Mensuration
Trigonometry
Mathematics

Graphical Representation of Data

Graphical Representation of Data: Graphical Representation of Data,” where numbers and facts become lively pictures and colorful diagrams . Instead of staring at boring lists of numbers, we use fun charts, cool graphs, and interesting visuals to understand information better. In this exciting concept of data visualization, we’ll learn about different kinds of graphs, charts, and pictures that help us see patterns and stories hidden in data.

There is an entire branch in mathematics dedicated to dealing with collecting, analyzing, interpreting, and presenting numerical data in visual form in such a way that it becomes easy to understand and the data becomes easy to compare as well, the branch is known as Statistics .

The branch is widely spread and has a plethora of real-life applications such as Business Analytics, demography, Astro statistics, and so on . In this article, we have provided everything about the graphical representation of data, including its types, rules, advantages, etc.

Table of Content

What is Graphical Representation

Types of graphical representations, line graphs, histograms , stem and leaf plot , box and whisker plot .

Graphical Representations used in Maths

Value-Based or Time Series Graphs

Frequency based, principles of graphical representations, advantages and disadvantages of using graphical system, general rules for graphical representation of data, frequency polygon, solved examples on graphical representation of data.

Graphics Representation is a way of representing any data in picturized form . It helps a reader to understand the large set of data very easily as it gives us various data patterns in visualized form.

There are two ways of representing data,

Pictorial Representation through graphs.

They say, “A picture is worth a thousand words”. It’s always better to represent data in a graphical format. Even in Practical Evidence and Surveys, scientists have found that the restoration and understanding of any information is better when it is available in the form of visuals as Human beings process data better in visual form than any other form.

Does it increase the ability 2 times or 3 times? The answer is it increases the Power of understanding 60,000 times for a normal Human being, the fact is amusing and true at the same time.

Check: Graph and its representations

Comparison between different items is best shown with graphs, it becomes easier to compare the crux of the data about different items. Let’s look at all the different types of graphical representations briefly:

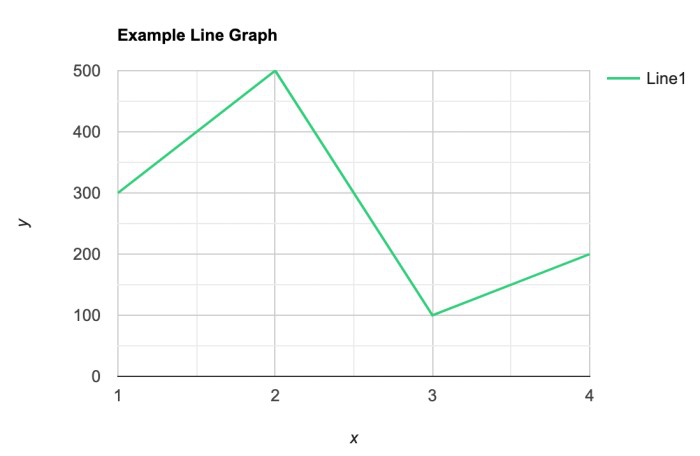
A line graph is used to show how the value of a particular variable changes with time. We plot this graph by connecting the points at different values of the variable. It can be useful for analyzing the trends in the data and predicting further trends.

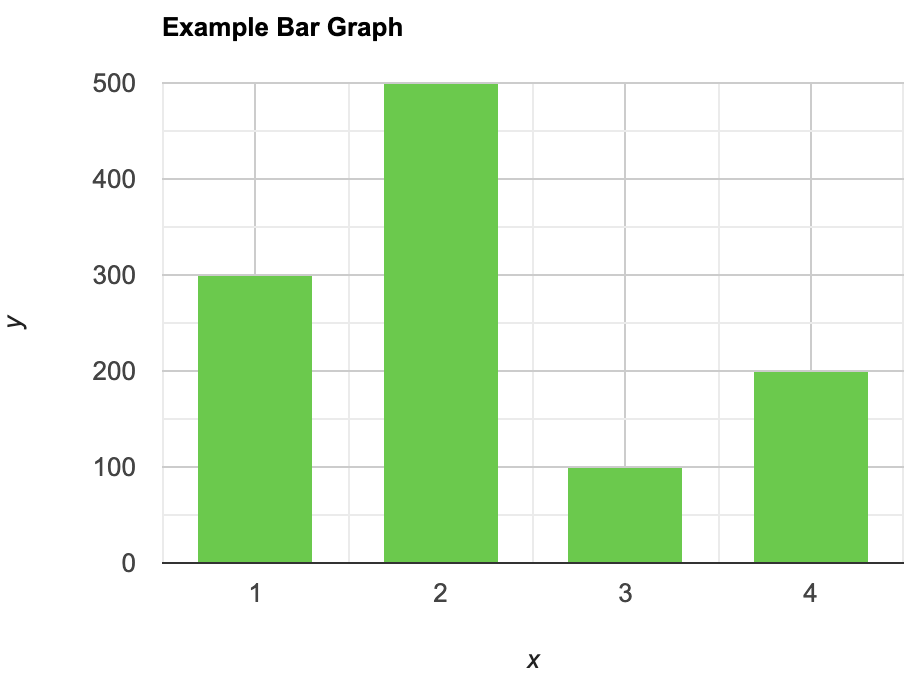
A bar graph is a type of graphical representation of the data in which bars of uniform width are drawn with equal spacing between them on one axis (x-axis usually), depicting the variable. The values of the variables are represented by the height of the bars.

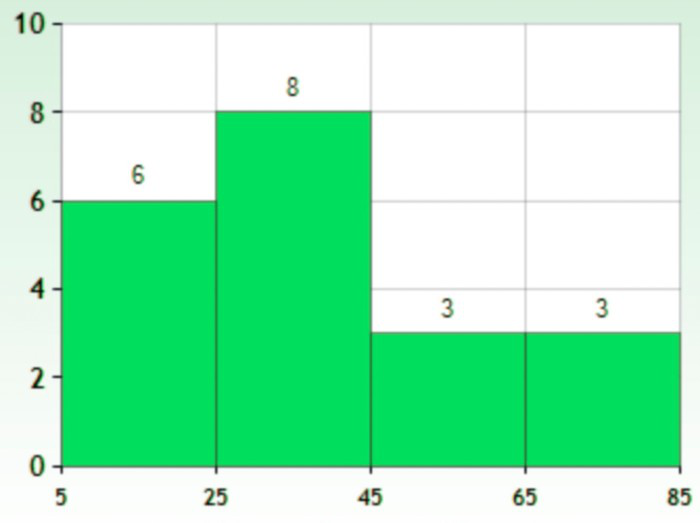
This is similar to bar graphs, but it is based frequency of numerical values rather than their actual values. The data is organized into intervals and the bars represent the frequency of the values in that range. That is, it counts how many values of the data lie in a particular range.

It is a plot that displays data as points and checkmarks above a number line, showing the frequency of the point.

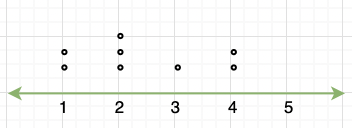
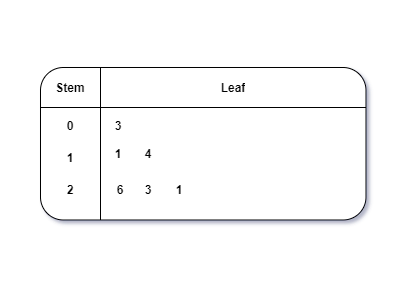
This is a type of plot in which each value is split into a “leaf”(in most cases, it is the last digit) and “stem”(the other remaining digits). For example: the number 42 is split into leaf (2) and stem (4).

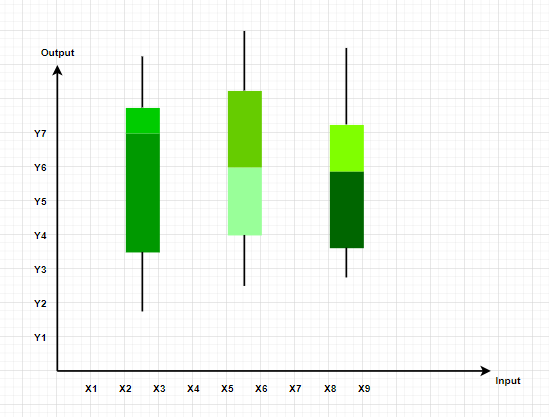
These plots divide the data into four parts to show their summary. They are more concerned about the spread, average, and median of the data.

It is a type of graph which represents the data in form of a circular graph. The circle is divided such that each portion represents a proportion of the whole.

Graphical Representations used in Math’s

Graphs in Math are used to study the relationships between two or more variables that are changing. Statistical data can be summarized in a better way using graphs. There are basically two lines of thoughts of making graphs in maths:

Value-Based or Time Series Graphs

These graphs allow us to study the change of a variable with respect to another variable within a given interval of time. The variables can be anything. Time Series graphs study the change of variable with time. They study the trends, periodic behavior, and patterns in the series. We are more concerned with the values of the variables here rather than the frequency of those values.

Example: Line Graph

These kinds of graphs are more concerned with the distribution of data. How many values lie between a particular range of the variables, and which range has the maximum frequency of the values. They are used to judge a spread and average and sometimes median of a variable under study.

Also read: Types of Statistical Data

All types of graphical representations follow algebraic principles.
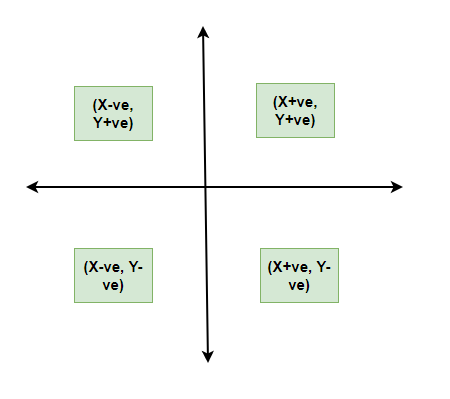
When plotting a graph, there’s an origin and two axes.
The x-axis is horizontal, and the y-axis is vertical.
The axes divide the plane into four quadrants.
The origin is where the axes intersect.
Positive x-values are to the right of the origin; negative x-values are to the left.
Positive y-values are above the x-axis; negative y-values are below.

It gives us a summary of the data which is easier to look at and analyze.
It saves time.
We can compare and study more than one variable at a time.

Disadvantages

It usually takes only one aspect of the data and ignores the other. For example, A bar graph does not represent the mean, median, and other statistics of the data.
Interpretation of graphs can vary based on individual perspectives, leading to subjective conclusions.
Poorly constructed or misleading visuals can distort data interpretation and lead to incorrect conclusions.

Check : Diagrammatic and Graphic Presentation of Data

We should keep in mind some things while plotting and designing these graphs. The goal should be a better and clear picture of the data. Following things should be kept in mind while plotting the above graphs:

Whenever possible, the data source must be mentioned for the viewer.
Always choose the proper colors and font sizes. They should be chosen to keep in mind that the graphs should look neat.
The measurement Unit should be mentioned in the top right corner of the graph.
The proper scale should be chosen while making the graph, it should be chosen such that the graph looks accurate.
Last but not the least, a suitable title should be chosen.

A frequency polygon is a graph that is constructed by joining the midpoint of the intervals. The height of the interval or the bin represents the frequency of the values that lie in that interval.

Question 1: What are different types of frequency-based plots?

Types of frequency-based plots: Histogram Frequency Polygon Box Plots

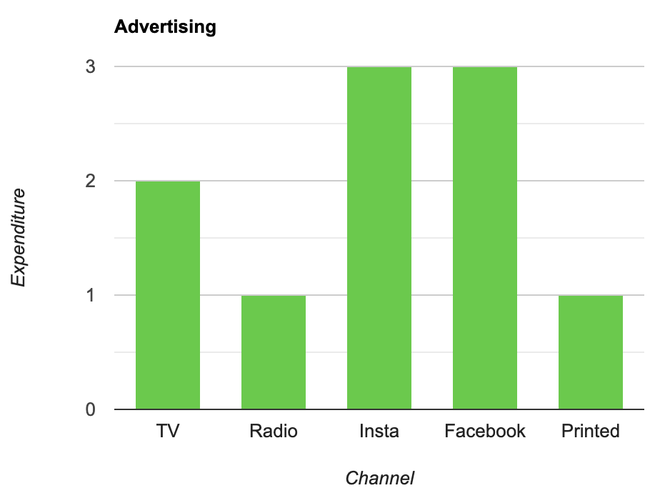
Question 2: A company with an advertising budget of Rs 10,00,00,000 has planned the following expenditure in the different advertising channels such as TV Advertisement, Radio, Facebook, Instagram, and Printed media. The table represents the money spent on different channels.

Draw a bar graph for the following data.

Put each of the channels on the x-axis
The height of the bars is decided by the value of each channel.

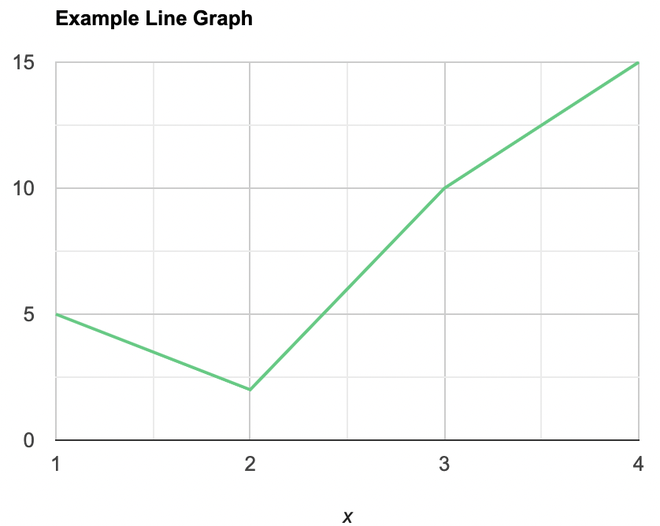
Question 3: Draw a line plot for the following data

Put each of the x-axis row value on the x-axis
joint the value corresponding to the each value of the x-axis.

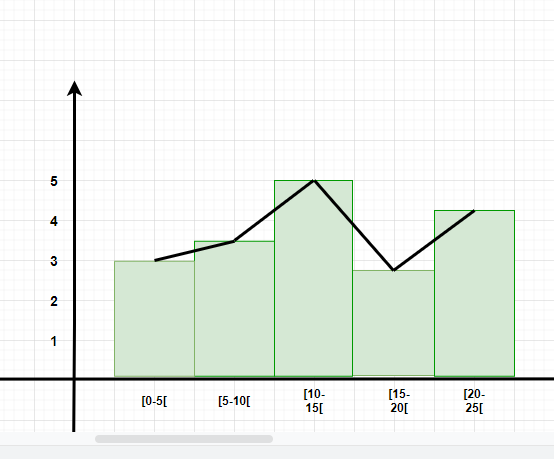
Question 4: Make a frequency plot of the following data:

Draw the class intervals on the x-axis and frequencies on the y-axis.
Calculate the midpoint of each class interval.

Now join the mid points of the intervals and their corresponding frequencies on the graph.

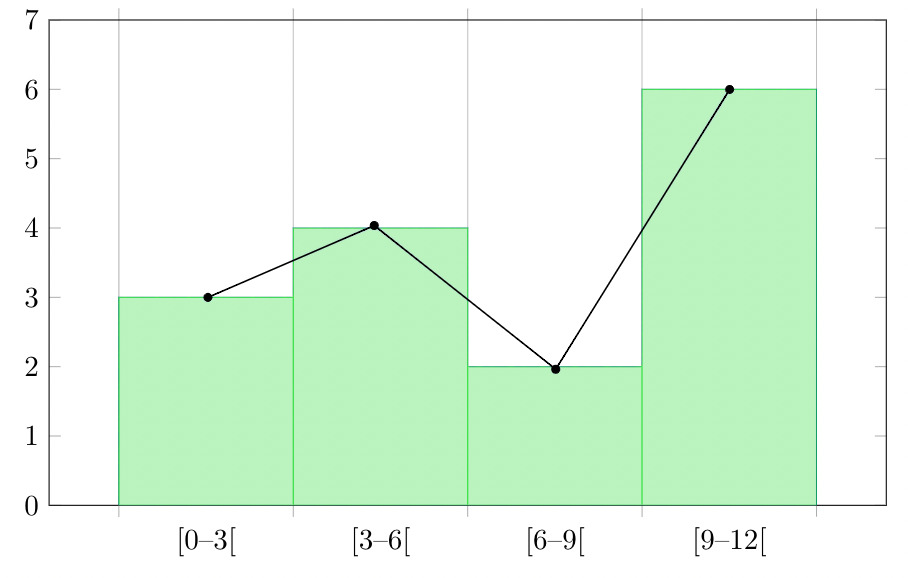
This graph shows both the histogram and frequency polygon for the given distribution.

Graphical Representation of Data| Practical Work in Geography Class 12 What are the different ways of Data Representation What are the different ways of Data Representation? Charts and Graphs for Data Visualization

Conclusion of Graphical Representation

Graphical representation is a powerful tool for understanding data, but it’s essential to be aware of its limitations. While graphs and charts can make information easier to grasp, they can also be subjective, complex, and potentially misleading . By using graphical representations wisely and critically, we can extract valuable insights from data, empowering us to make informed decisions with confidence.

Graphical Representation of Data – FAQs

What are the advantages of using graphs to represent data.

Graphs offer visualization, clarity, and easy comparison of data, aiding in outlier identification and predictive analysis.

What are the common types of graphs used for data representation?

Common graph types include bar, line, pie, histogram, and scatter plots , each suited for different data representations and analysis purposes.

How do you choose the most appropriate type of graph for your data?

Select a graph type based on data type, analysis objective, and audience familiarity to effectively convey information and insights.

How do you create effective labels and titles for graphs?

Use descriptive titles, clear axis labels with units, and legends to ensure the graph communicates information clearly and concisely.

How do you interpret graphs to extract meaningful insights from data?

Interpret graphs by examining trends, identifying outliers, comparing data across categories, and considering the broader context to draw meaningful insights and conclusions.

School Learning
Maths-Class-9

Chapter 1: Number System

Number System in Maths Number System is a method of representing numbers on the number line with the help of a set of Symbols and rules. These symbols range from 0-9 and are termed as digits. Let's learn about the number system in detail, including its types, and conversion. Number System in MathsNumber system in Maths is 13 min read
Natural Numbers | Definition, Examples & Properties Natural numbers are the numbers that start from 1 and end at infinity. In other words, natural numbers are counting numbers and they do not include 0 or any negative or fractional numbers. For example, 3, 6, 57, 973, 4000, and so on. Natural numbers are the counting numbers: 1, 2, 3, 4, 5, and so on 11 min read
Whole Numbers - Definition, Properties and Examples Whole numbers are a foundational concept in mathematics, encompassing all non-negative integers starting from zero. This set includes numbers like 0, 1, 2, 3, and so on, up to infinity. Unlike integers, whole numbers do not include negative numbers or fractions. Examples of Whole Numbers are 0, 2, 3 9 min read
Prime Numbers Prime numbers are those natural numbers divisible by only 1 and the number itself. Numbers with more than two factors are called composite numbers. All primes are odd numbers except for 2. A total of 25 prime numbers are there between 1 and 100. These are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 12 min read
Rational Numbers Rational numbers are a fundamental concept in mathematics, defined as numbers that can be expressed as the ratio of two integers, where the denominator is not zero. Represented in the form p/q (with p and q being integers), rational numbers include fractions, whole numbers, and terminating or repea 15+ min read
Irrational Numbers- Definition, Examples, Symbol, Properties Irrational numbers are real numbers that cannot be expressed as fractions. Irrational Numbers can not be expressed in the form of p/q, where p and q are integers and q ≠ 0. They are non-recurring, non-terminating, and non-repeating decimals. Irrational numbers are real numbers but are different from 12 min read
Real Numbers Real Numbers are continuous quantities that can represent a distance along a line, as Real numbers include both rational and irrational numbers. Rational numbers occupy the points at some finite distance and irrational numbers fill the gap between them, making them together to complete the real line 10 min read
Decimal Expansion of Real Numbers The combination of a set of rational and irrational numbers is called real numbers. All the real numbers can be expressed on the number line. The numbers other than real numbers that cannot be represented on the number line are called imaginary numbers (unreal numbers). They are used to represent co 6 min read
Decimal Expansions of Rational Numbers Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. So in this article let's discuss some rational and irrational numbers an 6 min read
Representation of Rational Numbers on the Number Line | Class 8 Maths Rational numbers are the integers p and q expressed in the form of p/q where q>0. Rational numbers can be positive, negative or even zero. Rational numbers can be depicted on the number line. The centre of the number line is called Origin (O). Positive rational numbers are illustrated on the righ 5 min read
Operations on Real Numbers Real Numbers are those numbers that are a combination of rational numbers and irrational numbers in the number system of maths. Real Number Operations include all the arithmetic operations like addition, subtraction, multiplication, etc. that can be performed on these numbers. Besides, imaginary num 9 min read
Rationalization of Denominators Rationalization of Denomintors is a method where we change the fraction with an irrational denominator into a fraction with a rational denominator. If there is an irrational or radical in the denominator the definition of rational number ceases to exist as we can't divide anything into irrational pa 8 min read
Nth Root Nth root of unity is the root of unity when taken which on taking to the power n gives the value 1. Nth root of any number is defined as the number that takes to the power of n results in the original number. For example, if we take the nth root of any number, say b, the result is a, and then a is r 7 min read
Laws of Exponents for Real Numbers Laws of Exponents are fundamental rules used in mathematics to simplify expressions involving exponents. These laws help in solving arithmetic problems efficiently by defining operations like multiplication, division, and more on exponents. In this article, we will discuss the laws of exponent for r 6 min read

Chapter 2: Polynomials

Polynomials in One Variable | Polynomials Class 9 Maths Polynomials in One Variable: Polynomial word originated from two words “poly” which means “many” and the word “nominal” which means “term”. In maths, a polynomial expression consists of variables known as indeterminate and coefficients. Polynomials are expressions with one or more terms with a non-z 7 min read
Polynomial Formula Polynomial Formula gives the standard form of polynomial expressions. It specifies the arrangement of algebraic expressions according to their increasing or decreasing power of variables. Let's learn about various polynomial formulas and identities in detail. Table of Content What is Polynomial?Type 6 min read
Types of Polynomials (Based on Terms and Degrees) Types of Polynomials: In mathematics, an algebraic expression is an expression built up from integer constants, variables, and algebraic operations. There are mainly four types of polynomials based on degree-constant polynomial (zero degree), linear polynomial ( 1st degree), quadratic polynomial (2n 9 min read
Zeros of Polynomial Zeros of a Polynomial are those real, imaginary, or complex values when put in the polynomial instead of a variable, the result becomes zero (as the name suggests zero as well). Polynomials are used to model some physical phenomena happening in real life, they are very useful in describing situation 14 min read
Factorization of Polynomial Factorization is the process in which we can find factors of either a given number or the algebraic expression using various techniques such as prime factorization, factorization using algebraic identities, and factorization of a quadratic polynomial using the middle term splitting method. Factoriza 12 min read
Remainder Theorem The Remainder Theorem is a simple yet powerful tool in algebra that helps you quickly find the remainder when dividing a polynomial by a linear polynomial, such as (x - a). Instead of performing long or synthetic division, you can use this theorem to substitute the polynomial and get the remainder d 9 min read
Factor Theorem Factor theorem is used for finding the roots of the given polynomial. This theorem is very helpful in finding the factors of the polynomial equation without actually solving them. According to the factor theorem, for any polynomial f(x) of degree n ≥ 1 a linear polynomial (x - a) is the factor of th 11 min read
Algebraic Identities Algebraic Identities are fundamental equations in algebra where the left-hand side of the equation is always equal to the right-hand side, regardless of the values of the variables involved. These identities play a crucial role in simplifying algebraic computations and are essential for solving vari 14 min read

Chapter 3: Coordinate Geometry

Coordinate Geometry Coordinate geometry is the branch of mathematics that deals with plotting the curve on the coordinate axes. Various curves can be plotted on the coordinate plane using coordinate geometry formulas. Co-ordinate geometry uses algebraic equations to plot various curves on the coordinate plane. One of t 11 min read
Cartesian Coordinate System Cartesian Coordinate System in Maths is a division of coordinate geometry where the location of a point in a plane or space is marked by a pair of numbers or three numbers. The branch of geometry that deals with the Cartesian Coordinate System is called Coordinate Geometry. The numbers which are use 15+ min read
Cartesian Plane Cartesian plane is defined as the two-dimensional plane used in the Cartesian coordinate system. This plane is formed by intersecting two perpendicular lines called the x-axis and the y-axis and their intersection is called the origin. This method of distributing the 2-Dimensional space into four ar 9 min read

Chapter 4: Linear equations in two variables

Linear Equations in One Variable Linear equation in one variable is the equation that is used in algebra for finding unknown quantities. It is used for representing the conditions that are dependent on one variable. It is a linear equation i.e. the equation in which the degree of the equation is one, and it only has one variable. L 8 min read
Linear Equation in Two Variables Linear Equation in Two Variables: A Linear equation is defined as an equation with the maximum degree of one only, for example, ax = b can be referred to as a linear equation, and when a Linear equation in two variables comes into the picture, it means that the entire equation has 2 variables presen 9 min read
Graph of Linear Equations in Two Variables Linear equations are the first-order equations, i.e. the equations of degree 1. The equations which are used to define any straight line are linear, they are represented as, x + k = 0; These equations have a unique solution and can be represented on number lines very easily. Let's look at linear e 5 min read
Graphical Methods of Solving Pair of Linear Equations in Two Variables A system of linear equations is just a pair of two lines that may or may not intersect. The graph of a linear equation is a line. There are various methods that can be used to solve two linear equations, for example, Substitution Method, Elimination Method, etc. An easy-to-understand and beginner-fr 8 min read

Chapter 5: Introduction to Euclid's Geometry

Euclidean Geometry Euclidean geometry is the study of 2-Dimensional geometrical shapes and figures. Euclidean geometry is based on different axioms and theorems. The word geometry is derived from the Greek words ‘geo’ meaning Earth and ‘metrein’ meaning ‘To measure’. Thus, geometry is the measure of the Earth or vario 15 min read
Equivalent Version of Euclid’s Fifth Postulate Geometry has originated from a variety of civilizations. Almost every major civilization has studied and used geometry in its prime. Egyptian and Indian civilizations were more focused on using geometry as a tool. Euclid came and changed the way people used to think in geometry. Instead of making it 6 min read

Chapter 6: Lines and Angles

Lines and Angles Lines and Angles are the basic terms used in the Geometry. They provide a base for understanding all the concepts of geometry. We define a line as a 1-D figure which can be extended to infinity in opposite directions, whereas an angle is defined as the opening created by joining two or more lines. A 10 min read
Types of Angles Types of Angles: An angle is a geometric figure formed by two rays meeting at a common endpoint. It is measured in degrees or radians. It deals with the relationship of points, lines, angles, and shapes in space. Understanding different types of angles is crucial for solving theoretical problems in 10 min read
Pairs of Angles - Lines & Angles When two lines share a common endpoint, called Vertex then an angle is formed between these two lines and when these angles appear in groups of two to display a specific geometrical property then they are called pairs of angles. Understanding these angle pairs helps in solving geometry problems invo 8 min read
Transversal Lines Transversal Lines in geometry is defined as a line that intersects two lines at distinct points in a plane. The transversal line intersecting a pair of parallel lines is responsible for the formation of various types of angles that, include alternate interior angles, corresponding angles, and others 7 min read
Angle Sum Property of a Triangle Angle Sum Property of a Triangle is the special property of a triangle that is used to find the value of an unknown angle in the triangle. It is the most widely used property of a triangle and according to this property, "Sum of All the Angles of a Triangle is equal to 180º." Angle Sum Property of a 8 min read

Chapter 7: Triangles

Triangles in Geometry A triangle is a polygon with three sides (edges), three vertices (corners), and three angles. It is the simplest polygon in geometry, and the sum of its interior angles is always 180°. A triangle is formed by three line segments (edges) that intersect at three vertices, creating a two-dimensional re 13 min read
Congruence of Triangles |SSS, SAS, ASA, and RHS Rules Congruence of triangles is a concept in geometry which is used to compare different shapes. It is the condition between two triangles in which all three corresponding sides and corresponding angles are equal. Two triangles are said to be congruent if and only if they can be overlapped with each othe 10 min read
Theorem - Angle opposite to equal sides of an isosceles triangle are equal | Class 9 Maths In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Exampl 4 min read
Triangle Inequality Theorem, Proof & Applications Triangle Inequality Theorem is the relation between the sides and angles of triangles which helps us understand the properties and solutions related to triangles. Triangles are the most fundamental geometric shape as we can't make any closed shape with two or one side. Triangles consist of three sid 9 min read

Chapter 8: Quadrilateral

Angle Sum Property of a Quadrilateral Angle Sum Property of a Quadrilateral: Quadrilaterals are encountered everywhere in life, every square rectangle, any shape with four sides is a quadrilateral. We know, three non-collinear points make a triangle. Similarly, four non-collinear points take up a shape that is called a quadrilateral. It 9 min read
Quadrilaterals Quadrilateral is a two-dimensional figure characterized by having four sides, four vertices, and four angles. It can be broadly classified into two categories: concave and convex. Within the convex category, there are several specific types of quadrilaterals, including trapezoids, parallelograms, re 12 min read
Parallelogram | Properties, Formulas, Types, and Theorem A parallelogram is a two-dimensional geometrical shape whose opposite sides are equal in length and are parallel. The opposite angles of a parallelogram are equal in measure and the Sum of adjacent angles of a parallelogram is equal to 180 degrees. A parallelogram is a four-sided polygon (quadrilate 10 min read
Rhombus: Definition, Properties, Formula and Examples A rhombus is a type of quadrilateral with the following additional properties. All four sides are of equal length and opposite sides parallel. The opposite angles are equal, and the diagonals bisect each other at right angles. A rhombus is a special case of a parallelogram, and if all its angles are 7 min read
Trapezium in Maths | Formulas, Properties & Examples A trapezium or Trapezoid is a four-sided quadrilateral with one pair of parallel sides, called the bases, and the other two non-parallel sides called the legs. The term "trapezium" comes from the Greek word "trapeze," meaning "table."It is a two-dimensional shape with four sides and four vertices. T 8 min read
Square in Maths - Area, Perimeter, Examples & Applications A square is a type of quadrilateral where all four sides are of equal length and each interior angle measures 90°. It has two pairs of parallel sides, with opposite sides being parallel. The diagonals of a square are equal in length and bisect each other at right angles.Squares are used in various f 6 min read
Kite - Quadrilaterals A Kite is a special type of quadrilateral that is easily recognizable by its unique shape, resembling the traditional toy flown on a string. In geometry, a kite has two pairs of adjacent sides that are of equal length. This distinctive feature sets it apart from other quadrilaterals like squares, re 8 min read
Properties of Parallelograms Properties of Parallelograms: Parallelogram is a quadrilateral in which opposite sides are parallel and congruent and the opposite angles are equal. A parallelogram is formed by the intersection of two pairs of parallel lines. In this article, we will learn about the properties of parallelograms, in 9 min read
Mid Point Theorem The Midpoint Theorem is a fundamental concept in geometry that simplifies solving problems involving triangles. It establishes a relationship between the midpoints of two sides of a triangle and the third side. This theorem is especially useful in coordinate geometry and in proving other mathematica 6 min read

Chapter 9: Areas of Parallelograms and Triangles

Area of a Triangle | Formula and Examples The area of the triangle is a basic geometric concept that calculates the measure of the space enclosed by the three sides of the triangle. The formulas to find the area of a triangle include the base-height formula, Heron's formula, and trigonometric methods. The area of triangle is generally calcu 6 min read
Area of Parallelogram | Definition, Formulas & Examples The area of a Parallelogram is the space or the region enclosed by the boundary of the parallelogram in a two-dimensional space. It is calculated by multiplying the base of the parallelogram by its height. In this article, we will learn more about the Area of Parallelogram Formulas, and how to use t 10 min read
Figures on the Same Base and between the Same Parallels A triangle is a three-sided polygon and a parallelogram is a four-sided polygon or simply a quadrilateral that has parallel opposite sides. We encounter these two polynomials almost everywhere in our everyday lives. For example: Let's say a farmer has a piece of land that is in the shape of a parall 6 min read

Chapter 10: Circles

Circles in Maths A circle is a two-dimensional shape where all points on the circumference are the same distance from the center. A circle consists of all points in a plane that are equidistant (at the same distance) from a fixed point called the centre. The distance from the centre to any point on the circle is cal 10 min read
Radius of Circle Radius of Circle: The radius of a circle is the distance from the circle's center to any point on its circumference. It is commonly represented by 'R' or 'r'. The radius is crucial in nearly all circle-related formulas, as the area and circumference of a circle are also calculated using the radius. 8 min read
Tangent to a Circle Tangent in Circles are the line segments that touch the given curve only at one particular point. Tangent is a Greek word meaning "To Touch". For a circle, we can say that the line which touches the circle from the outside at one single point on the circumference is called the tangent of the circle. 10 min read
What is the longest chord of a Circle? Geometry OverviewGeometry is the major part of mathematics that deals with lines, angles, points, etc. They are the visual study of shapes and sizes. The geometric approach is seen everywhere around us as every object has a certain shape whose parameters can be studied with the help of geometrical f 5 min read
Circumference of Circle - Definition, Perimeter Formula, and Examples The circumference of a circle is the distance around its boundary, much like the perimeter of any other shape. It is a key concept in geometry, particularly when dealing with circles in real-world applications such as measuring the distance traveled by wheels or calculating the boundary of round obj 8 min read
Angle subtended by an arc at the centre of a circle Given the angle subtended by an arc at the circle circumference X, the task is to find the angle subtended by an arc at the centre of a circle.For eg in the below given image, you are given angle X and you have to find angle Y. Examples: Input: X = 30 Output: 60Input: X = 90 Output: 180 Approach: Wh 3 min read
What is Cyclic Quadrilateral Cyclic Quadrilateral is a special type of quadrilateral in which all the vertices of the quadrilateral lie on the circumference of a circle. In other words, if you draw a quadrilateral and then find a circle that passes through all four vertices of that quadrilateral, then that quadrilateral is call 9 min read
The sum of opposite angles of a cyclic quadrilateral is 180° | Class 9 Maths Theorem In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the cir 6 min read

Chapter 11: Construction

Basic Constructions - Angle Bisector, Perpendicular Bisector, Angle of 60° Most of the time we use diagrams while depicting the shapes and scenarios in mathematics. But they are not precise, they are just a representation of the actual shape without proper measurements. But when we are building something like a wooden table, or map of a building is to be constructed. It ne 5 min read
Construction of Triangles Triangles are three-sided polygon which have three vertices. Basic construction techniques allow us to construct triangles. An important property of the triangle is that sum of internal angles of a triangle is 180°. SAS, SSS, ASA, and RHS are the rules of congruency of two triangles. A triangle is 8 min read

Chapter 12: Heron's Formula

Area of Equilateral Triangle The area of an equilateral triangle is the amount of space enclosed within its three equal sides. For an equilateral triangle, where all three sides and all three internal angles are equal (each angle measuring 60 degrees), the area can be calculated using the formula [Tex]\frac{\sqrt{3}}{4}\times a 6 min read
Area of Isosceles Triangle Area of Isosceles triangle is the space enclosed by the sides of a triangle. The general formula for finding the area of the isosceles triangle is given by half the product of the base and height of the triangle. Other than this different formulas are used to find the area of triangles. Triangles ar 10 min read
Heron's Formula Heron's formula is a popular method for calculating the area of a triangle when the lengths of its three sides are known. It was introduced by Heron of Alexandria in his book "Metrica". This formula applies to all types of triangles, including right-angled, equilateral, and isosceles. According to t 9 min read
Applications of Heron's Formula While solving and finding the Area of a Triangle, Certain parameters are expected to be provided beforehand, for example, the height and the base of the triangle must be available Or in the case of an Equilateral Triangle, the lengths of the side should be given. Heron's formula is basically for a t 10 min read
Area of Quadrilateral Area of Quadrilateral: The Area of a quadrilateral is the space inside the boundary of a quadrilateral or in other words, the space enclosed by the edges of a quadrilateral. A quadrilateral is a closed two-dimensional shape with four sides or edges, and also four corners or vertices. In mensuration, 11 min read
Area of Polygons Area of the Polygon is the area enclosed by the boundary of the polygon. A polygon is a closed, two-dimensional shape with straight sides. Each side of a polygon is a line segment, and the points where the sides meet are called vertices. A polygon is a figure formed by joining 'n' straight lines suc 15 min read

Chapter 13: Surface Areas and Volumes

Surface Area of Cuboid The surface area of a cuboid is the total space occupied by all its surfaces/sides. In geometry, a three-dimensional shape having six rectangular faces is called a cuboid. A cuboid is also known as a regular hexahedron and has six rectangular faces, eight vertices, and twelve edges with congruent, o 12 min read
Volume of Cuboid | Formula and Examples Volume of a cuboid is calculated using the formula V = L × B × H, where V represents the volume in cubic units, L stands for length, B for breadth, and H for height. Here, the breadth and width of a cuboid are the same things. The volume signifies the amount of space occupied by the cuboid in three 8 min read
Surface Area of Cube | Curved & Total Surface Area Surface area of a cube is defined as the total area covered by all the faces of a cube. In geometry, the cube is a fascinating three-dimensional object that we encounter daily, from dice to ice cubes. But have you ever wondered about the total area that covers a cube? This is what we call the surfac 15 min read
Volume of a Cube Volume of a Cube is defined as the total number of cubic units occupied by the cube completely. A cube is a three-dimensional solid figure, having 6 square faces. Volume is nothing but the total space occupied by an object. An object with a larger volume would occupy more space. The volume of the cu 9 min read
Surface Area of Cylinder | Curved and Total Surface Area of Cylinder Surface Area of a Cylinder is the amount of space covered by the flat surface of the cylinder's bases and the curved surface of the cylinder. The total surface area of the cylinder includes the area of the cylinder's two circular bases as well as the area of the curving surface. The volume of a cyli 10 min read
Volume of a Cylinder| Formula, Definition and Examples Volume of a cylinder is a fundamental concept in geometry and plays a crucial role in various real-life applications. It is a measure which signifies the amount of material the cylinder can carry. It is also defined as the space occupied by the Cylinder. The formula for the volume of a cylinder is π 11 min read
Surface Area of Cone Surface Area of a Cone is the total area encompassing the circular base and the curved surface of the cone. A cone has two types of surface areas. If the radius of the base is 'r' and the slant height is 'l', we use two formulas: Total Surface Area (TSA) of the cone = πr(r + l)Curved Surface Area (C 8 min read
Volume of Cone- Formula, Derivation and Examples Volume of a cone can be defined as the space occupied by the cone. As we know, a cone is a three-dimensional geometric shape with a circular base and a single apex (vertex). Let's learn about Volume of Cone in detail, including its Formula, Examples, and the Frustum of Cone. Volume of ConeA cone's v 10 min read
Surface Area of Sphere | Formula, Derivation and Solved Examples A sphere is a three-dimensional object with all points on its surface equidistant from its center, giving it a perfectly round shape. The surface area of a sphere is the total area that covers its outer surface. To calculate the surface area of a sphere with radius r, we use the formula: Surface Are 8 min read
Volume of a Sphere The volume of a sphere helps us understand how much space a perfectly round object occupies, from tiny balls to large planets. Using the simple volume of sphere formula, you can easily calculate the space inside any sphere. Whether you're curious about the volume of a solid sphere in math or science 8 min read
Surface Area of a Hemisphere A hemisphere is a 3D shape that is half of a sphere's volume and surface area. The surface area of a hemisphere comprises both the curved region and the base area combined. Hemisphere's Total Surface Area (TSA) = Curved Surface Area + Base Area = 3πr² square units.Curved Surface Area (CSA) = 2πr² sq 13 min read
Volume of Hemisphere Volume of a shape is defined as how much capacity a shape has or we can say how much material was required to form that shape. A hemisphere, derived from the Greek words "hemi" (meaning half) and "sphere," is simply half of a sphere. If you imagine slicing a perfectly round sphere into two equal hal 6 min read

Chapter 14: Statistics

Collection and Presentation of Data We come across a lot of information every day from different sources. Our newspapers, TV, Phone and the Internet, etc are the sources of information in our life. This information can be related to anything, from bowling averages in cricket to profits of the company over the years. These facts and fi 10 min read
Graphical Representation of Data Graphical Representation of Data: Graphical Representation of Data," where numbers and facts become lively pictures and colorful diagrams. Instead of staring at boring lists of numbers, we use fun charts, cool graphs, and interesting visuals to understand information better. In this exciting concept 8 min read
Bar Graphs and Histograms A Bar graph or a Histogram is a tool used for visual representation of data. Representing the data in a bar graphs or histograms, makes it easy to understand the concepts and relationships among data. A Histogram is used to display the distribution of continuous data by grouping values into interval 6 min read
Central Tendency in Statistics- Mean, Median, Mode Central Tendencies are the numerical values that are used to represent a large collection of numerical data. These obtained numerical values are called central or average values. A central or average value of any statistical data or series is the variable's value representative of the entire data or 9 min read
Mean, Median and Mode Mean, Median, and Mode are measures of the central tendency. These values are used to define the various parameters of the given data set. The measure of central tendency (Mean, Median, and Mode) gives useful insights about the data studied, these are used to study any type of data such as the avera 15 min read

Chapter 15: Probability

Experimental Probability Experimental probability, also known as empirical probability, is a concept in mathematics that deals with estimating the likelihood of an event occurring based on actual experimental results. Unlike theoretical probability, which predicts outcomes based on known possibilities, experimental probabil 8 min read
Empirical Probability Empirical Probability: Probability describes the chance that an uncertain event will occur. Empirical probability is based on how likely an event has occurred in the past. It is also called experimental probability. It is based on the relative frequency approach. We can get our results from experien 7 min read
CBSE Class 9 Maths Formulas GeeksforGeeks present Maths Chapterwise Formulas for Class 9. This is designed for the convenience of the students so that one can understand all the important concepts of Class 9 Mathematics directly and easily. Math formulae for Class 9 are offered here for students who find the topic of mathemati 15+ min read
NCERT Solutions for Class 9 Maths 2024-25: Chapter Wise PDF Download NCERT Solutions for Class 9 Maths offers complete answers to all questions in the NCERT textbook, covering topics like Number Systems, Coordinate Geometry, Polynomials, Euclid's Geometry, Quadrilaterals, Triangles, Circles, Constructions, Surface Areas, Volumes, Statistics, and Probability. If you a 15+ min read
RD Sharma Class 9 Solutions RD Sharma Solutions for class 9 provides vast knowledge about the concepts through the chapter-wise solutions. These solutions help to solve problems of higher difficulty and to ensure students have a good practice of all types of questions that can be framed in the examination. Referring to the sol 10 min read

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Math Article

Graphical Representation

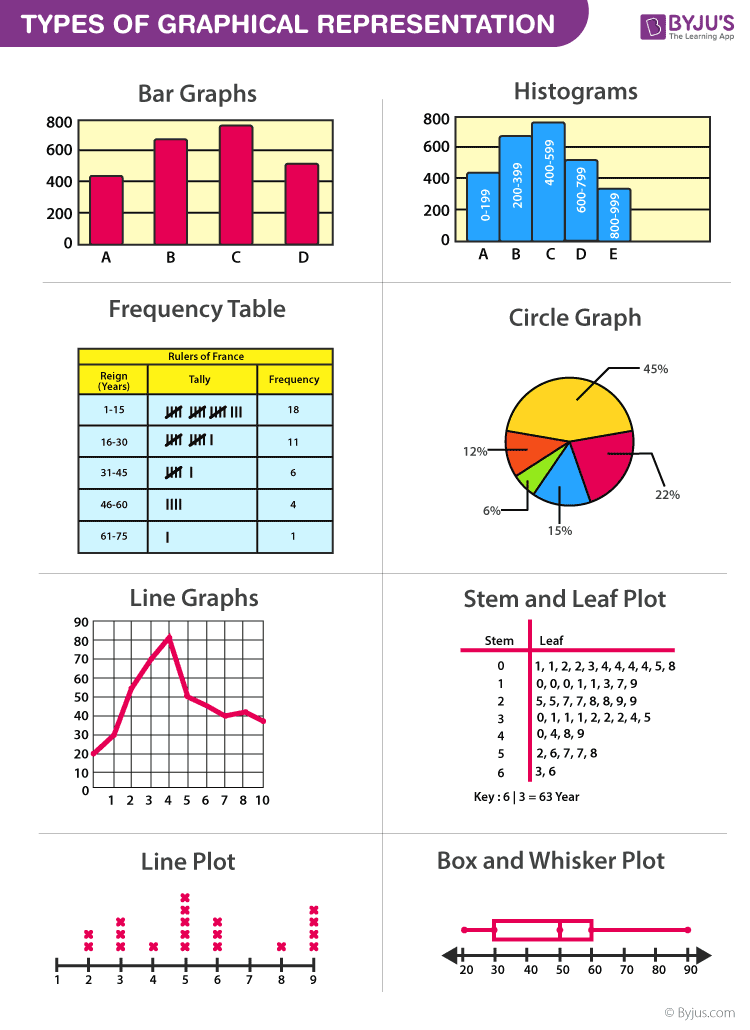
Graphical Representation is a way of analysing numerical data. It exhibits the relation between data, ideas, information and concepts in a diagram. It is easy to understand and it is one of the most important learning strategies. It always depends on the type of information in a particular domain. There are different types of graphical representation. Some of them are as follows:

Line Graphs – Line graph or the linear graph is used to display the continuous data and it is useful for predicting future events over time.
Bar Graphs – Bar Graph is used to display the category of data and it compares the data using solid bars to represent the quantities.
Histograms – The graph that uses bars to represent the frequency of numerical data that are organised into intervals. Since all the intervals are equal and continuous, all the bars have the same width.
Line Plot – It shows the frequency of data on a given number line. ‘ x ‘ is placed above a number line each time when that data occurs again.
Frequency Table – The table shows the number of pieces of data that falls within the given interval.
Circle Graph – Also known as the pie chart that shows the relationships of the parts of the whole. The circle is considered with 100% and the categories occupied is represented with that specific percentage like 15%, 56%, etc.
Stem and Leaf Plot – In the stem and leaf plot, the data are organised from least value to the greatest value. The digits of the least place values from the leaves and the next place value digit forms the stems.
Box and Whisker Plot – The plot diagram summarises the data by dividing into four parts. Box and whisker show the range (spread) and the middle ( median) of the data.

General Rules for Graphical Representation of Data

There are certain rules to effectively present the information in the graphical representation. They are:

Suitable Title: Make sure that the appropriate title is given to the graph which indicates the subject of the presentation.
Measurement Unit: Mention the measurement unit in the graph.
Proper Scale: To represent the data in an accurate manner, choose a proper scale.
Index: Index the appropriate colours, shades, lines, design in the graphs for better understanding.
Data Sources: Include the source of information wherever it is necessary at the bottom of the graph.
Keep it Simple: Construct a graph in an easy way that everyone can understand.
Neat: Choose the correct size, fonts, colours etc in such a way that the graph should be a visual aid for the presentation of information.

Graphical Representation in Maths

In Mathematics, a graph is defined as a chart with statistical data, which are represented in the form of curves or lines drawn across the coordinate point plotted on its surface. It helps to study the relationship between two variables where it helps to measure the change in the variable amount with respect to another variable within a given interval of time. It helps to study the series distribution and frequency distribution for a given problem. There are two types of graphs to visually depict the information. They are:

Time Series Graphs – Example: Line Graph
Frequency Distribution Graphs – Example: Frequency Polygon Graph

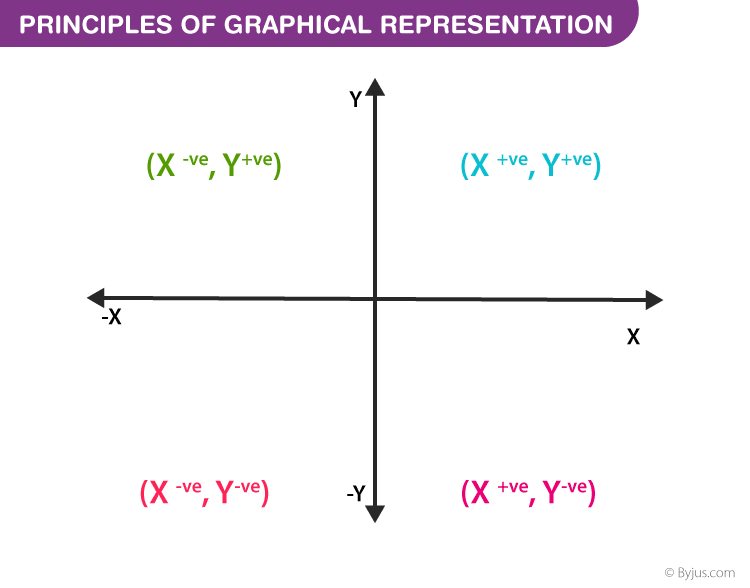
Principles of Graphical Representation

Algebraic principles are applied to all types of graphical representation of data. In graphs, it is represented using two lines called coordinate axes. The horizontal axis is denoted as the x-axis and the vertical axis is denoted as the y-axis. The point at which two lines intersect is called an origin ‘O’. Consider x-axis, the distance from the origin to the right side will take a positive value and the distance from the origin to the left side will take a negative value. Similarly, for the y-axis, the points above the origin will take a positive value, and the points below the origin will a negative value.

Generally, the frequency distribution is represented in four methods, namely

Smoothed frequency graph
Pie diagram
Cumulative or ogive frequency graph
Frequency Polygon

Merits of Using Graphs

Some of the merits of using graphs are as follows:

The graph is easily understood by everyone without any prior knowledge.
It saves time
It allows us to relate and compare the data for different time periods
It is used in statistics to determine the mean, median and mode for different data, as well as in the interpolation and the extrapolation of data.

Example for Frequency polygonGraph

Here are the steps to follow to find the frequency distribution of a frequency polygon and it is represented in a graphical way.

Obtain the frequency distribution and find the midpoints of each class interval.
Represent the midpoints along x-axis and frequencies along the y-axis.
Plot the points corresponding to the frequency at each midpoint.
Join these points, using lines in order.
To complete the polygon, join the point at each end immediately to the lower or higher class marks on the x-axis.

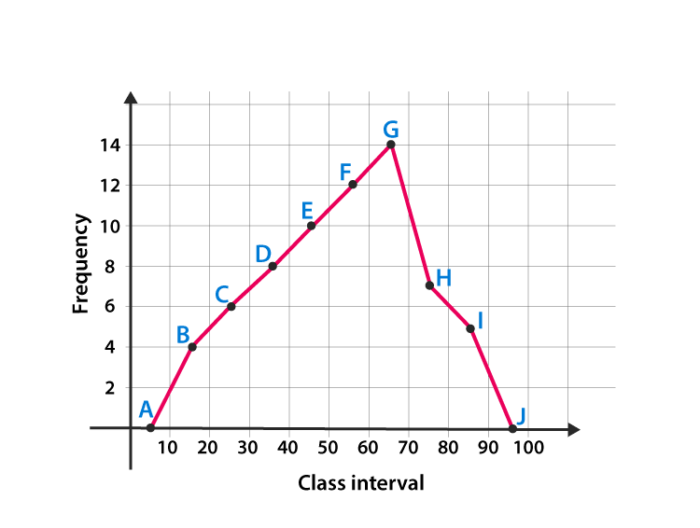
Draw the frequency polygon for the following data

Mark the class interval along x-axis and frequencies along the y-axis.

Let assume that class interval 0-10 with frequency zero and 90-100 with frequency zero.

Now calculate the midpoint of the class interval.

Using the midpoint and the frequency value from the above table, plot the points A (5, 0), B (15, 4), C (25, 6), D (35, 8), E (45, 10), F (55, 12), G (65, 14), H (75, 7), I (85, 5) and J (95, 0).

To obtain the frequency polygon ABCDEFGHIJ, draw the line segments AB, BC, CD, DE, EF, FG, GH, HI, IJ, and connect all the points.

Frequently Asked Questions

What are the different types of graphical representation.

Some of the various types of graphical representation include:

Line Graphs
Frequency Table
Circle Graph, etc.

What are the Advantages of Graphical Method?

Some of the advantages of graphical representation are:

It makes data more easily understandable.
It saves time.
It makes the comparison of data more efficient.

Register with BYJU'S & Download Free PDFs

Types of Graphs and Charts And Their Uses

If you are wondering what are the different types of graphs and charts , their uses and names, this page summarizes them with examples and pictures.

Although it is hard to tell what are all the types of graphs, this page consists all of the common types of statistical graphs and charts (and their meanings) widely used in any science.

1. Line Graphs

A line chart graphically displays data that changes continuously over time. Each line graph consists of points that connect data to show a trend (continuous change). Line graphs have an x-axis and a y-axis. In the most cases, time is distributed on the horizontal axis.

Uses of line graphs:

When you want to show trends . For example, how house prices have increased over time.
When you want to make predictions based on a data history over time.
When comparing two or more different variables, situations, and information over a given period of time.

The following line graph shows annual sales of a particular business company for the period of six consecutive years:

Note: the above example is with 1 line. However, one line chart can compare multiple trends by several distributing lines.

2. Bar Charts

Bar charts represent categorical data with rectangular bars (to understand what is categorical data see categorical data examples ). Bar graphs are among the most popular types of graphs and charts in economics, statistics, marketing, and visualization in digital customer experience . They are commonly used to compare several categories of data.

Each rectangular bar has length and height proportional to the values that they represent.

One axis of the bar chart presents the categories being compared. The other axis shows a measured value.

Bar Charts Uses:

When you want to display data that are grouped into nominal or ordinal categories (see nominal vs ordinal data ).
To compare data among different categories.
Bar charts can also show large data changes over time.
Bar charts are ideal for visualizing the distribution of data when we have more than three categories.

The bar chart below represents the total sum of sales for Product A and Product B over three years.

The bars are 2 types: vertical or horizontal. It doesn’t matter which kind you will use. The above one is a vertical type.

3. Pie Charts

When it comes to statistical types of graphs and charts, the pie chart (or the circle chart) has a crucial place and meaning. It displays data and statistics in an easy-to-understand ‘pie-slice’ format and illustrates numerical proportion.

Each pie slice is relative to the size of a particular category in a given group as a whole. To say it in another way, the pie chart brakes down a group into smaller pieces. It shows part-whole relationships.

To make a pie chart, you need a list of categorical variables and numerical variables.

Pie Chart Uses:

When you want to create and represent the composition of something.
It is very useful for displaying nominal or ordinal categories of data.
To show percentage or proportional data.
When comparing areas of growth within a business such as profit.
Pie charts work best for displaying data for 3 to 7 categories.

The pie chart below represents the proportion of types of transportation used by 1000 students to go to their school.

Pie charts are widely used by data-driven marketers for displaying marketing data.

4. Histogram

A histogram shows continuous data in ordered rectangular columns (to understand what is continuous data see our post discrete vs continuous data ). Usually, there are no gaps between the columns.

The histogram displays a frequency distribution (shape) of a data set. At first glance, histograms look alike to bar graphs. However, there is a key difference between them. Bar Chart represents categorical data and histogram represent continuous data.

Histogram Uses:

When the data is continuous .
When you want to represent the shape of the data’s distribution .
When you want to see whether the outputs of two or more processes are different.
To summarize large data sets graphically.
To communicate the data distribution quickly to others.

The histogram below represents per capita income for five age groups.

Histograms are very widely used in statistics, business, and economics.

5. Scatter plot

The scatter plot is an X-Y diagram that shows a relationship between two variables. It is used to plot data points on a vertical and a horizontal axis. The purpose is to show how much one variable affects another.

Usually, when there is a relationship between 2 variables, the first one is called independent. The second variable is called dependent because its values depend on the first variable.

Scatter plots also help you predict the behavior of one variable (dependent) based on the measure of the other variable (independent).

Scatter plot uses:

When trying to find out whether there is a relationship between 2 variables .
To predict the behavior of dependent variable based on the measure of the independent variable.
When having paired numerical data.
When working with root cause analysis tools to identify the potential for problems.
When you just want to visualize the correlation between 2 large datasets without regard to time .

The below Scatter plot presents data for 7 online stores, their monthly e-commerce sales, and online advertising costs for the last year.

The orange line you see in the plot is called “line of best fit” or a “trend line”. This line is used to help us make predictions that are based on past data.

The Scatter plots are used widely in data science and statistics. They are a great tool for visualizing linear regression models .

More examples and explanation for scatter plots you can see in our post what does a scatter plot show and simple linear regression examples .

6. Venn Chart

Venn Diagram (also called primary diagram, set diagram or logic diagrams) uses overlapping circles to visualize the logical relationships between two or more group of items.

Venn Diagram is one of the types of graphs and charts used in scientific and engineering presentations, in computer applications, in maths, and in statistics.

The basic structure of the Venn diagram is usually overlapping circles. The items in the overlapping section have specific common characteristics. Items in the outer portions of the circles do not have common traits.

Venn Chart Uses:

When you want to compare and contrast groups of things.
To categorize or group items.
To illustrate logical relationships from various datasets.
To identify all the possible relationships between collections of datasets.

The following science example of Venn diagram compares the features of birds and bats.

7. Area Charts

Area Chart Uses:

When you want to show trends , rather than express specific values.
To show a simple comparison of the trend of data sets over the period of time.
To display the magnitude of a change.
To compare a small number of categories.

The area chart has 2 variants: a variant with data plots overlapping each other and a variant with data plots stacked on top of each other (known as stacked area chart – as the shown in the following example).

The area chart below shows quarterly sales for product categories A and B for the last year.

This area chart shows you a quick comparison of the trend in the quarterly sales of Product A and Product B over the period of the last year.

8. Spline Chart

The Spline Chart is one of the most widespread types of graphs and charts used in statistics. It is a form of the line chart that represent smooth curves through the different data points.

Spline charts possess all the characteristics of a line chart except that spline charts have a fitted curved line to join the data points. In comparison, line charts connect data points with straight lines.

Spline Chart Uses:

When you want to plot data that requires the usage of curve-fitting such as a product lifecycle chart or an impulse-response chart.
Spline charts are often used in designing Pareto charts .
Spline chart also is often used for data modeling by when you have limited number of data points and estimating the intervening values.

The following spline chart example shows sales of a company through several months of a year:

9. Box and Whisker Chart

A box and whisker chart is a statistical graph for displaying sets of numerical data through their quartiles. It displays a frequency distribution of the data.

The box and whisker chart helps you to display the spread and skewness for a given set of data using the five number summary principle: minimum, maximum, median, lower and upper quartiles. The ‘five-number summary’ principle allows providing a statistical summary for a particular set of numbers. It shows you the range (minimum and maximum numbers), the spread (upper and lower quartiles), and the center (median) for the set of data numbers.

A very simple figure of a box and whisker plot you can see below:

Box and Whisker Chart Uses:

When you want to observe the upper, lower quartiles, mean, median, deviations, etc. for a large set of data.
When you want to see a quick view of the dataset distribution .
When you have multiple data sets that come from independent sources and relate to each other in some way.
When you need to compare data from different categories.

The table and box-and-whisker plots below shows test scores for Maths and Literature for the same class.

Box and Whisker charts have applications in many scientific areas and types of analysis such as statistical analysis, test results analysis, marketing analysis, data analysis, and etc.

10. Bubble Chart

Bubble charts are super useful types of graphs for making a comparison of the relationships between data in 3 numeric-data dimensions: the Y-axis data, the X-axis data, and data depicting the bubble size.

Bubble charts are very similar to XY Scatter plots but the bubble chart adds more functionality – a third dimension of data that can be extremely valuable.

Both axes (X and Y) of a bubble chart are numeric.

Bubble Chart Uses:

When you have to display three or four dimensions of data.
When you want to compare and display the relationships between categorized circles, by the use of proportions.

The bubble chart below shows the relationship between Cost (X-Axis), Profit (Y-Axis), and Probability of Success (%) (Bubble Size).

11. Pictographs

The pictograph or a pictogram is one of the more visually appealing types of graphs and charts that display numerical information with the use of icons or picture symbols to represent data sets.

They are very easy to read statistical way of data visualization. A pictogram shows the frequency of data as images or symbols. Each image/symbol may represent one or more units of a given dataset.

Pictograph Uses:

When your audience prefers and understands better displays that include icons and illustrations. Fun can promote learning.
It’s habitual for infographics to use of a pictogram.
When you want to compare two points in an emotionally powerful way.

The following pictographic represents the number of computers sold by a business company for the period from January to March.

The pictographic example above shows that in January are sold 20 computers (4×5 = 20), in February are sold 30 computers (6×5 = 30) and in March are sold 15 computers.

12. Dot Plot

Dot plot or dot graph is just one of the many types of graphs and charts to organize statistical data. It uses dots to represent data. A Dot Plot is used for relatively small sets of data and the values fall into a number of discrete categories.

If a value appears more than one time, the dots are ordered one above the other. That way the column height of dots shows the frequency for that value.

Dot Plot Uses:

To plot frequency counts when you have a small number of categories .
Dot plots are very useful when the variable is quantitative or categorical .
Dot graphs are also used for univariate data (data with only one variable that you can measure).

Suppose you have a class of 26 students. They are asked to tell their favorite color. The dot plot below represents their choices:

It is obvious that blue is the most preferred color by the students in this class.

13. Radar Chart

A radar chart is one of the most modern types of graphs and charts – ideal for multiple comparisons. Radar charts use a circular display with several different quantitative axes looking like spokes on a wheel. Each axis shows a quantity for a different categorical value.

Radar charts are also known as spider charts, web charts, star plots, irregular polygons, polar charts, cobweb charts or Kiviat diagram.

Radar Chart has many applications nowadays in statistics, maths, business, sports analysis, data intelligence, and etc.

Radar Chart Uses:

When you want to observe which variables have similar values or whether there are any outliers amongst each variable.
To represent multiple comparisons .
When you want to see which variables are scoring low or high within a dataset. This makes radar chart ideal for displaying performance .

For example, we can compare employee’s performance with the scale of 1-8 on subjects such as Punctuality, Problem-solving, Meeting Deadlines, Marketing Knowledge, Communications. A point that is closer to the center on an axis shows a lower value and a worse performance.

It is obvious that Jane has a better performance than Samanta.

14. Pyramid Graph

When it comes to easy to understand and good looking types of graphs and charts, pyramid graph has a top place.

A pyramid graph is a chart in a pyramid shape or triangle shape. These types of charts are best for data that is organized in some kind of hierarchy. The levels show a progressive order.

Pyramid Graph Uses:

When you want to indicate a hierarchy level among the topics or other types of data.
Pyramid graph is often used to represent progressive orders such as: “older to newer”, “more important to least important”, “specific to least specific”‘ and etc.
When you have a proportional or interconnected relationship between data sets.

A classic pyramid graph example is the healthy food pyramid that shows fats, oils, and sugar (at the top) should be eaten less than many other foods such as vegetables and fruits (at the bottom of the pyramid).

Conclusion:

You might know that choosing the right type of chart is some kind of tricky business.

Anyway, you have a wide choice of types of graphs and charts. Used in the right way, they are a powerful weapon to help you make your reports and presentations both professional and clear.

What are your favorite types of graphs and charts? Share your thoughts on the field below.

About The Author

Silvia Valcheva

Silvia Valcheva is a digital marketer with over a decade of experience creating content for the tech industry. She has a strong passion for writing about emerging software and technologies such as big data, AI (Artificial Intelligence), IoT (Internet of Things), process automation, etc.

10 Comments

I have learned a lot from your presentation. Very informative

Nicely described different graphs, I learned a lot.

very useful. exiting

I love this. I learned a lot.

Very good representation of date. I would suggest an addition of “stem and leaf” diagrams.

I have only one thing to say and that is this is the best representation of every graphs and charts I have ever seen 😀

Very well described. Great learning article for beginners on Charts.

Really helpful thanks

Very Helpful text; Thanks Silvia Valcheva for your hard work

Graphical Representation of Data

Graphical representation of data is an attractive method of showcasing numerical data that help in analyzing and representing quantitative data visually. A graph is a kind of a chart where data are plotted as variables across the coordinate. It became easy to analyze the extent of change of one variable based on the change of other variables. Graphical representation of data is done through different mediums such as lines, plots, diagrams, etc. Let us learn more about this interesting concept of graphical representation of data, the different types, and solve a few examples.

Definition of Graphical Representation of Data

A graphical representation is a visual representation of data statistics-based results using graphs, plots, and charts. This kind of representation is more effective in understanding and comparing data than seen in a tabular form. Graphical representation helps to qualify, sort, and present data in a method that is simple to understand for a larger audience. Graphs enable in studying the cause and effect relationship between two variables through both time series and frequency distribution. The data that is obtained from different surveying is infused into a graphical representation by the use of some symbols, such as lines on a line graph, bars on a bar chart, or slices of a pie chart. This visual representation helps in clarity, comparison, and understanding of numerical data.

Representation of Data

The word data is from the Latin word Datum, which means something given. The numerical figures collected through a survey are called data and can be represented in two forms - tabular form and visual form through graphs. Once the data is collected through constant observations, it is arranged, summarized, and classified to finally represented in the form of a graph. There are two kinds of data - quantitative and qualitative. Quantitative data is more structured, continuous, and discrete with statistical data whereas qualitative is unstructured where the data cannot be analyzed.

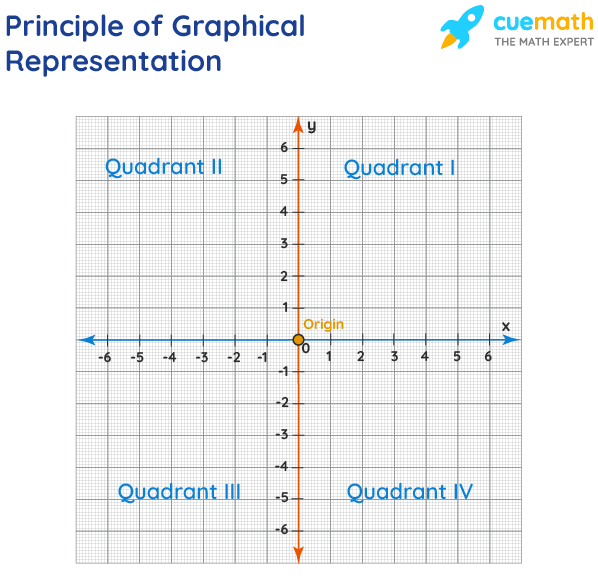
Principles of Graphical Representation of Data

The principles of graphical representation are algebraic. In a graph, there are two lines known as Axis or Coordinate axis. These are the X-axis and Y-axis. The horizontal axis is the X-axis and the vertical axis is the Y-axis. They are perpendicular to each other and intersect at O or point of Origin. On the right side of the Origin, the Xaxis has a positive value and on the left side, it has a negative value. In the same way, the upper side of the Origin Y-axis has a positive value where the down one is with a negative value. When -axis and y-axis intersect each other at the origin it divides the plane into four parts which are called Quadrant I, Quadrant II, Quadrant III, Quadrant IV. This form of representation is seen in a frequency distribution that is represented in four methods, namely Histogram, Smoothed frequency graph, Pie diagram or Pie chart, Cumulative or ogive frequency graph, and Frequency Polygon.

Principle of Graphical Representation of Data

Advantages and Disadvantages of Graphical Representation of Data

Listed below are some advantages and disadvantages of using a graphical representation of data:

It improves the way of analyzing and learning as the graphical representation makes the data easy to understand.
It can be used in almost all fields from mathematics to physics to psychology and so on.
It is easy to understand for its visual impacts.
It shows the whole and huge data in an instance.
It is mainly used in statistics to determine the mean, median, and mode for different data

The main disadvantage of graphical representation of data is that it takes a lot of effort as well as resources to find the most appropriate data and then represent it graphically.

Rules of Graphical Representation of Data

While presenting data graphically, there are certain rules that need to be followed. They are listed below:

Suitable Title: The title of the graph should be appropriate that indicate the subject of the presentation.
Measurement Unit: The measurement unit in the graph should be mentioned.
Proper Scale: A proper scale needs to be chosen to represent the data accurately.
Index: For better understanding, index the appropriate colors, shades, lines, designs in the graphs.
Data Sources: Data should be included wherever it is necessary at the bottom of the graph.
Simple: The construction of a graph should be easily understood.
Neat: The graph should be visually neat in terms of size and font to read the data accurately.

Uses of Graphical Representation of Data

The main use of a graphical representation of data is understanding and identifying the trends and patterns of the data. It helps in analyzing large quantities, comparing two or more data, making predictions, and building a firm decision. The visual display of data also helps in avoiding confusion and overlapping of any information. Graphs like line graphs and bar graphs, display two or more data clearly for easy comparison. This is important in communicating our findings to others and our understanding and analysis of the data.

Types of Graphical Representation of Data

Data is represented in different types of graphs such as plots, pies, diagrams, etc. They are as follows,

Examples on Graphical Representation of Data

Example 1 : A pie chart is divided into 3 parts with the angles measuring as 2x, 8x, and 10x respectively. Find the value of x in degrees.

We know, the sum of all angles in a pie chart would give 360º as result. ⇒ 2x + 8x + 10x = 360º ⇒ 20 x = 360º ⇒ x = 360º/20 ⇒ x = 18º Therefore, the value of x is 18º.

Example 2: Ben is trying to read the plot given below. His teacher has given him stem and leaf plot worksheets. Can you help him answer the questions? i) What is the mode of the plot? ii) What is the mean of the plot? iii) Find the range.

Solution: i) Mode is the number that appears often in the data. Leaf 4 occurs twice on the plot against stem 5.

Hence, mode = 54

ii) The sum of all data values is 12 + 14 + 21 + 25 + 28 + 32 + 34 + 36 + 50 + 53 + 54 + 54 + 62 + 65 + 67 + 83 + 88 + 89 + 91 = 958

To find the mean, we have to divide the sum by the total number of values.

Mean = Sum of all data values ÷ 19 = 958 ÷ 19 = 50.42

iii) Range = the highest value - the lowest value = 91 - 12 = 79

go to slide go to slide

Book a Free Trial Class

Practice Questions on Graphical Representation of Data

Faqs on graphical representation of data, what is graphical representation.

Graphical representation is a form of visually displaying data through various methods like graphs, diagrams, charts, and plots. It helps in sorting, visualizing, and presenting data in a clear manner through different types of graphs. Statistics mainly use graphical representation to show data.

What are the Different Types of Graphical Representation?

The different types of graphical representation of data are:

Stem and leaf plot
Scatter diagrams
Frequency Distribution

Is the Graphical Representation of Numerical Data?

Yes, these graphical representations are numerical data that has been accumulated through various surveys and observations. The method of presenting these numerical data is called a chart. There are different kinds of charts such as a pie chart, bar graph, line graph, etc, that help in clearly showcasing the data.

What is the Use of Graphical Representation of Data?

Graphical representation of data is useful in clarifying, interpreting, and analyzing data plotting points and drawing line segments , surfaces, and other geometric forms or symbols.

What are the Ways to Represent Data?

Tables, charts, and graphs are all ways of representing data, and they can be used for two broad purposes. The first is to support the collection, organization, and analysis of data as part of the process of a scientific study.

What is the Objective of Graphical Representation of Data?

The main objective of representing data graphically is to display information visually that helps in understanding the information efficiently, clearly, and accurately. This is important to communicate the findings as well as analyze the data.

Guide On Graphical Representation of Data – Types, Importance, Rules, Principles And Advantages

What are Graphs and Graphical Representation?

Graphs, in the context of data visualization, are visual representations of data using various graphical elements such as charts, graphs, and diagrams. Graphical representation of data , often referred to as graphical presentation or simply graphs which plays a crucial role in conveying information effectively.

Principles of Graphical Representation

Effective graphical representation follows certain fundamental principles that ensure clarity, accuracy, and usability:Clarity : The primary goal of any graph is to convey information clearly and concisely. Graphs should be designed in a way that allows the audience to quickly grasp the key points without confusion.

Simplicity: Simplicity is key to effective data visualization. Extraneous details and unnecessary complexity should be avoided to prevent confusion and distraction.
Relevance: Include only relevant information that contributes to the understanding of the data. Irrelevant or redundant elements can clutter the graph.
Visualization: Select a graph type that is appropriate for the supplied data. Different graph formats, like bar charts, line graphs, and scatter plots, are appropriate for various sorts of data and relationships.

Rules for Graphical Representation of Data

Creating effective graphical representations of data requires adherence to certain rules:

Select the Right Graph: Choosing the appropriate type of graph is essential. For example, bar charts are suitable for comparing categories, while line charts are better for showing trends over time.
Label Axes Clearly: Axis labels should be descriptive and include units of measurement where applicable. Clear labeling ensures the audience understands the data’s context.
Use Appropriate Colors: Colors can enhance understanding but should be used judiciously. Avoid overly complex color schemes and ensure that color choices are accessible to all viewers.
Avoid Misleading Scaling: Scale axes appropriately to prevent exaggeration or distortion of data. Misleading scaling can lead to incorrect interpretations.
Include Data Sources: Always provide the source of your data. This enhances transparency and credibility.

Importance of Graphical Representation of Data

Graphical representation of data in statistics is of paramount importance for several reasons:

Enhances Understanding: Graphs simplify complex data, making it more accessible and understandable to a broad audience, regardless of their statistical expertise.
Helps Decision-Making: Visual representations of data enable informed decision-making. Decision-makers can easily grasp trends and insights, leading to better choices.
Engages the Audience: Graphs capture the audience’s attention more effectively than raw data. This engagement is particularly valuable when presenting findings or reports.
Universal Language: Graphs serve as a universal language that transcends linguistic barriers. They can convey information to a global audience without the need for translation.

Advantages of Graphical Representation

The advantages of graphical representation of data extend to various aspects of communication and analysis:

Clarity: Data is presented visually, improving clarity and reducing the likelihood of misinterpretation.
Efficiency: Graphs enable the quick absorption of information. Key insights can be found in seconds, saving time and effort.
Memorability: Visuals are more memorable than raw data. Audiences are more likely to retain information presented graphically.
Problem-Solving: Graphs help in identifying and solving problems by revealing trends, correlations, and outliers that may require further investigation.

Use of Graphical Representations

Graphical representations find applications in a multitude of fields:

Business: In the business world, graphs are used to illustrate financial data, track performance metrics, and present market trends. They are invaluable tools for strategic decision-making.
Science: Scientists employ graphs to visualize experimental results, depict scientific phenomena, and communicate research findings to both colleagues and the general public.
Education: Educators utilize graphs to teach students about data analysis, statistics, and scientific concepts. Graphs make learning more engaging and memorable.
Journalism: Journalists rely on graphs to support their stories with data-driven evidence. Graphs make news articles more informative and impactful.

Types of Graphical Representation

There exists a diverse array of graphical representations, each suited to different data types and purposes. Common types include:

1.Bar Charts:

Used to compare categories or discrete data points, often side by side.

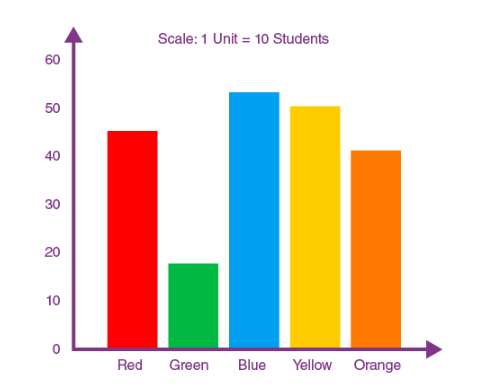
2. Line Charts:

Ideal for showing trends and changes over time, such as stock market performance or temperature fluctuations.

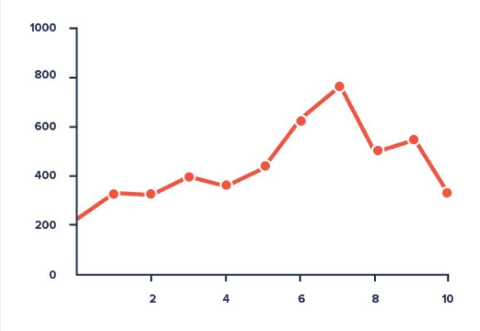
3. Pie Charts:

Display parts of a whole, useful for illustrating proportions or percentages.

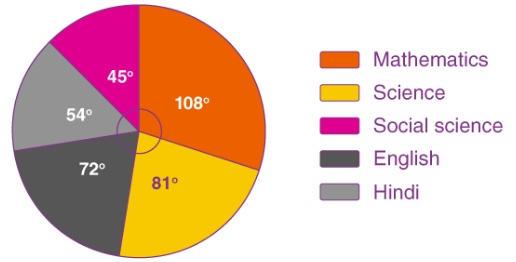
4. Scatter Plots:

Reveal relationships between two variables and help identify correlations.

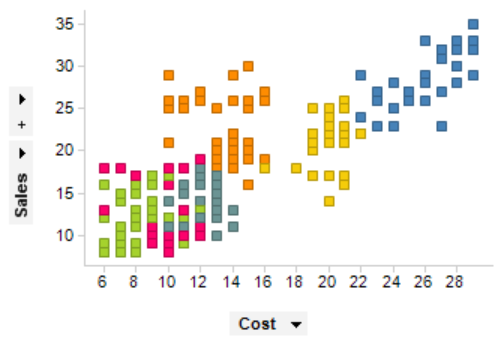
5. Histograms:

Depict the distribution of data, especially in the context of continuous variables.

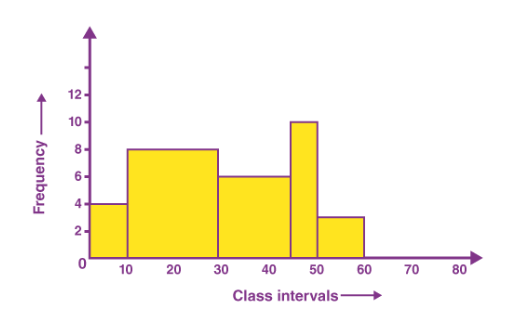
In conclusion, the graphical representation of data is an indispensable tool for simplifying complex information, aiding in decision-making, and enhancing communication across diverse fields. By following the principles and rules of effective data visualization, individuals and organizations can harness the power of graphs to convey their messages, support their arguments, and drive informed actions.

Download PPT of Graphical Representation

Video On Graphical Representation

FAQs on Graphical Representation of Data

What is the purpose of graphical representation.

Graphical representation serves the purpose of simplifying complex data, making it more accessible and understandable through visual means.

Why are graphs and diagrams important?

Graphs and diagrams are crucial because they provide visual clarity, aiding in the comprehension and retention of information.

How do graphs help learning?

Graphs engage learners by presenting information visually, which enhances understanding and retention, particularly in educational settings.

Who uses graphs?

Professionals in various fields, including scientists, analysts, educators, and business leaders, use graphs to convey data effectively and support decision-making.

Where are graphs used in real life?

Graphs are used in real-life scenarios such as business reports, scientific research, news articles, and educational materials to make data more accessible and meaningful.

Why are graphs important in business?

In business, graphs are vital for analyzing financial data, tracking performance metrics, and making informed decisions, contributing to success.

Cancel reply.

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Best Google AdWords Consultants in India...

What is a Google Ads Consultant? A Google Ads Consultant is an expert who specializes in delivering expertise and advice on Google Ads, which is Google’s online advertising medium. Google Ads permits companies to develop and run ads that are visible on Google’s search engine and other Google platforms. The function of a Google Ads […]

Best PPC Consultants in India –...

What Is a PPC Consultant? A PPC consultant or a pay per click consultant is an expert who specializes in handling and optimizing PPC advertisement drives for companies. PPC is a digital marketing model where advertisers pay a price each time their ad is clicked. Standard PPC mediums include Bing Ads, Google Ads, and social media advertisement platforms like […]

Top 20 Generic Digital Marketing Interview...

1. What is Digital Marketing? Digital marketing is also known as online marketing which means promoting and selling products or services to potential customers using the internet and online platforms. It includes email, social media, and web-based advertising, but also text and multimedia messages as a marketing channel. 2. What are the types of Digital […]

Best Social Media Consultants in India...

What Is a Social Media Consultant? A social media advisor is a specialist who delivers direction, recommendation, and assistance linked to the usage of social media for people, companies, or associations. Their prime objective is to support customers effectively by employing social media platforms to gain specific objectives, such as improving brand awareness, entertaining target […]

Gaurav Mittal

Had a great time spent with some awesome learning at The Digital Education Institute. It really helped me to build my career and i am thankful to the institute for making me what i am today.

Company where our students are working

Enroll Now for 2 Hour Free Digital Marketing Class

Lorem Ipsum is simply dummy text of the printing and typesetting industry

Lorem Ipsum is simply dummy text of the printing and typesetting industry . Lorem Ipsum is simply dummy text of the printing and typesetting industry

IMAGES

Graphical Representation: Types, Rules, Principles & Examples
Graphical Representation
Graphical Representation
Graphical Representation
Graphical Representation
Types of Graphical Representation Class 10 Maths Chapter 23 Notes

COMMENTS

Graphical Representation of Data | Graphs, Types of Graphs ...">Graphical Representation of Data | Graphs, Types of Graphs ...
Jun 5, 2024 · Common graph types include bar, line, pie, histogram, and scatter plots, each suited for different data representations and analysis purposes. How do you choose the most appropriate type of graph for your data?
Graphical Representation - Types, Rules, Principles and Merits">Graphical Representation - Types, Rules, Principles and Merits
There are different types of graphical representation. Some of them are as follows: Line Graphs – Line graph or the linear graph is used to display the continuous data and it is useful for predicting future events over time.
Types of Graphs and Charts And Their Uses - Intellspot">Types of Graphs and Charts And Their Uses - Intellspot
Every type of graph is a visual representation of data on diagram plots (ex. bar, pie, line chart) that show different types of graph trends and relationships between variables.
Graphical Representation, Its Advantages & Uses - Embibe">Graphical Representation, Its Advantages & Uses - Embibe
Jun 22, 2023 · Let’s study different kinds of graphical representations with examples, the types of graphical representation, and graphical representation of data in statistics, in this article. What Are Graphical Representations? Graphical representation refers to the use of intuitive charts to visualise clearly and simplify data sets.
Graphical Representation of Data - Cuemath">Graphical Representation of Data - Cuemath
What are the Different Types of Graphical Representation? The different types of graphical representation of data are: Bar graph; Line graph; Histogram; Pie chart; Stem and leaf plot; Pictograph; Scatter diagrams; Frequency Distribution; Is the Graphical Representation of Numerical Data? Yes, these graphical representations are numerical data ...
Graphical Representation: Types, Rules, Principles & Examples">Graphical Representation: Types, Rules, Principles & Examples
May 17, 2023 · A graphical representation is a visual representation of data based on the results using graphs, plots and charts. The graph is just a well-organised representation of data. What are the different types of graphical representations?
Graphical Representation Of Data | Types and ...">What Is Graphical Representation Of Data | Types and ...
Sep 15, 2023 · Different graph formats, like bar charts, line graphs, and scatter plots, are appropriate for various sorts of data and relationships. Creating effective graphical representations of data requires adherence to certain rules: Select the Right Graph: Choosing the appropriate type of graph is essential.

What is Graphical Representation

Value-Based or Time Series Graphs

Graphical Representations used in Math’s

Disadvantages

Related Article:

Conclusion of Graphical Representation

Graphical Representation of Data – FAQs

What are the common types of graphs used for data representation?

How do you choose the most appropriate type of graph for your data?

How do you create effective labels and titles for graphs?

How do you interpret graphs to extract meaningful insights from data?

Similar Reads

Chapter 1: Number System

Chapter 2: Polynomials

Chapter 3: Coordinate Geometry

Chapter 4: Linear equations in two variables

Chapter 5: Introduction to Euclid's Geometry

Chapter 6: Lines and Angles

Chapter 7: Triangles

Chapter 8: Quadrilateral

Chapter 9: Areas of Parallelograms and Triangles

Chapter 10: Circles

Chapter 11: Construction

Chapter 12: Heron's Formula

Chapter 13: Surface Areas and Volumes

Chapter 14: Statistics

Chapter 15: Probability

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Graphical Representation

General Rules for Graphical Representation of Data

Graphical Representation in Maths

Principles of Graphical Representation

Merits of Using Graphs

Example for Frequency polygonGraph

Frequently Asked Questions

What are the Advantages of Graphical Method?

Leave a Comment Cancel reply

Register with BYJU'S & Download Free PDFs

Types of Graphs and Charts And Their Uses

About The Author

Silvia Valcheva

10 Comments

Leave a Reply Cancel Reply

Graphical Representation of Data

Definition of Graphical Representation of Data

Representation of Data

Principles of Graphical Representation of Data

Advantages and Disadvantages of Graphical Representation of Data

Rules of Graphical Representation of Data

Uses of Graphical Representation of Data

Types of Graphical Representation of Data

Related Topics

Examples on Graphical Representation of Data

Practice Questions on Graphical Representation of Data

What are the Different Types of Graphical Representation?

Is the Graphical Representation of Numerical Data?

What is the Use of Graphical Representation of Data?

What are the Ways to Represent Data?

What is the Objective of Graphical Representation of Data?

Guide On Graphical Representation of Data – Types, Importance, Rules, Principles And Advantages

What are Graphs and Graphical Representation?

Principles of Graphical Representation

Rules for Graphical Representation of Data

Importance of Graphical Representation of Data

Advantages of Graphical Representation

Use of Graphical Representations

Types of Graphical Representation

1.Bar Charts:

2. Line Charts:

3. Pie Charts:

4. Scatter Plots:

5. Histograms:

Download PPT of Graphical Representation

Video On Graphical Representation

FAQs on Graphical Representation of Data

Why are graphs and diagrams important?

How do graphs help learning?

Who uses graphs?

Where are graphs used in real life?