probabilidad experimental significado

Probabilidad experimental

Aquí encontrarás el significado de la probabilidad experimental y cómo se calcula la probabilidad experimental. Además, podrás ver un ejemplo resuelto paso a paso del cálculo de la probabilidad experimental.

¿Qué es la probabilidad experimental?

La probabilidad experimental es una medida estadística que se basa en los resultados de un experimento o en hechos empíricos e indica la probabilidad de ocurrencia de un evento.

Además, cuantas más veces se haga el experimento, más precisa será la probabilidad experimental obtenida. Por esta razón se suelen utilizar programas informáticos capaces de simular miles de experimentos rápidamente para determinar la probabilidad experimental, así se consigue una mejor precisión.

La probabilidad experimental también se conoce como probabilidad empírica o probabilidad frecuencial .

La probabilidad experimental es un número entre 0 y 1. Lógicamente, cuanto más grande sea el valor de la probabilidad experimental de un evento más probable será de que suceda, y al revés, cuanto más pequeño sea el valor menos probable será de que ocurra el evento. Pero el valor de la probabilidad experimental siempre estará entre cero y uno.

Fórmula de la probabilidad experimental

La fórmula de la probabilidad experimental es el número de veces que ocurrió un evento durante un experimento partido por el número total de veces que se ha realizado el experimento.

Por ejemplo, si una persona tira diez dardos en una diana y consigue clavar 6 dardos en el cento, la probabilidad de que esa persona acierte un dardo en el centro se calcula de la siguiente manera:

Ejemplo de la probabilidad experimental

Una vez hemos visto la definición matemática de probabilidad experimental, a continuación resolveremos un ejercicio paso a paso de este tipo de probabilidad. El objetivo es que aprendas cómo se calcula la probabilidad experimental de un evento, por lo que si al final tienes alguna duda puedes escribirla en los comentarios.

• Calcula la probabilidad experimental de los eventos elementales que componen el experimento aleatorio de lanzar un dado.

Antes de encontrar la probabilidad experimental, calcularemos la probabilidad teórica para ir comparando los resultados experimentales obtenidos con los resultados teóricos. Como bien sabes, existen seis posibles resultados al lanzar un dado (1, 2, 3, 4, 5 y 6), así que la probabilidad teórica de cada evento elemental es:

Para resolver este ejercicio tenemos que simular el lanzamiento de un dado muchas veces y anotar los resultados en una tabla de contingencia. En este caso haremos las simulaciones con el programa Excel, pero evidentemente tú puedes usar el programa que quieras.

Primero simularemos diez lanzamientos, luego cien lanzamientos, y finalmente mil lanzamientos. De esta forma podremos ir analizando los resultados y ver cómo cambian según el tamaño de la muestra del experimento. Los resultados conseguidos después de simular aleatoriamente 10 lanzamientos de un dado son los siguientes:

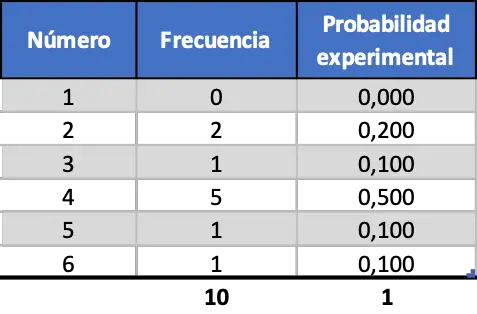
Como puedes comprobar, de momento las probabilidades experimentales obtenidas son bastante distintas a las probabilidades teóricas calculadas anteriormente (0,167).

Pero a medida que aumentamos el número de pruebas estas dos medidas se parecen más, fíjate en la simulación de 100 lanzamientos:

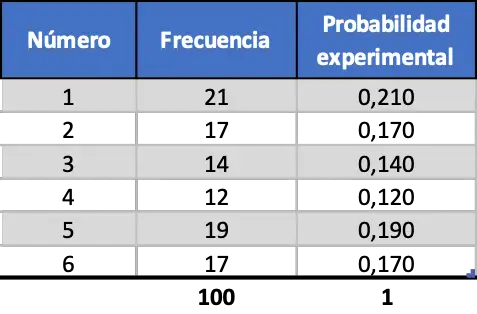
Ahora la probabilidad experimental se parece más al valor de la probabilidad teórica, sin embargo, aún obtenemos algunos valores lejanos.

Por último, hacemos el mismo procedimiento pero simulando 1000 lanzamientos:

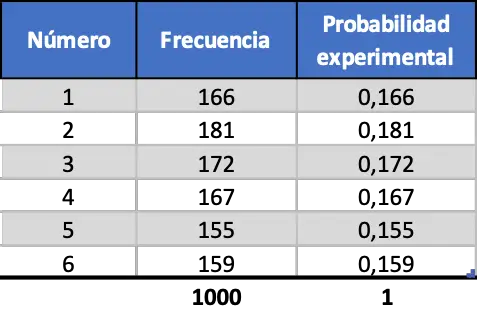
Como puedes ver en la última tabla de contingencia, ahora los valores de las probabilidades experimentales son muy similares a las probabilidades teóricas.

En resumen, cuanto mayor sea el número de experimentos realizados, más próximo será el valor de la probabilidad experimental de un evento a su probabilidad teórica . Esta regla se define como la ley de los números grandes , que establece que cuantos más datos haya, más próximos serán los valores experimentales a los valores teóricos.

Asimismo, si comparas las tres tablas de frecuencias, verás que la probabilidad experimental no es definitiva, sino que va cambiando según el número de experimentos realizados. Lo que significa que debemos saber interpretar los valores obtenidos.

Probabilidad experimental y probabilidad teórica

La diferencia entre la probabilidad experimental y la probabilidad teórica (o probabilidad clásica) es que la probabilidad experimental se calcula a partir de los datos recopilados de un experimento real, en cambio, la probabilidad teórica se calcula sin necesidad de hacer ningún experimento.

Como hemos visto, debemos simular un gran número de experimentos para sacar la probabilidad experimental de un evento. Sin embargo, el cálculo de la probabilidad teórica se hace a partir de la teoría y de la lógica. Puedes ver cómo se hace aquí:

Deja un comentario Cancelar respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Correo electrónico*

• Biología
• Química
• Ecología y Medio ambiente
• Ciencias sociales
• Matemáticas
• Psicología
• Salud y enfermería

Probabilidad experimental: definición y predicciones

Probabilidad experimental.

¿Has jugado alguna vez con una baraja de cartas? Si no es así, ¿ha tirado alguna vez un dado? O al menos, ¡estoy seguro de que has lanzado una moneda antes! Todos estos pueden aplicar el concepto de probabilidad experimental , que es la relación entre el número de veces que ocurre un resultado y el número total de veces que se realiza la actividad. ¡Repasemos este concepto usando monedas, mazos y dados!

Lanzar una moneda

Si lanza una moneda, hay dos resultados posibles: cara o cruz. Si lanza una moneda 100 veces, al menos en teoría, es probable que aparezcan caras 50 veces, o la mitad de las veces. Es decir, nuestra probabilidad teórica de voltear cabezas es ½ o 50%. Pero esto puede no ocurrir en la práctica, en un experimento real basado en pruebas y observación.

Esto es lo que quiero decir. Saca una moneda para mí. Esperaré. Bien, lanza la moneda 10 veces y anota la cantidad de veces que salgas cara en este experimento. Hice el experimento y salí cara 7 de cada 10 veces. En mi caso, ¿cuál es la probabilidad experimental de que al lanzar una moneda salga cara? 7 de cada 10, o el 70% del tiempo. Tal vez mi moneda no sea justa, o tal vez solo sea el azar lo que produjo este resultado. Sin embargo, si lanzáramos una moneda justa mil veces, las probabilidades experimentales se acercarían más a coincidir con las probabilidades teóricas.

Lanzar un dado y elegir una carta

Ahora, juguemos con un dado. En la pantalla podemos ver cómo se lanza el dado. En un experimento de 10 tiradas del dado, aparece un 3 4 veces. ¿Cuál es la probabilidad experimental de sacar un 3? Es 4 de 10, o 2/5, o 0,4, o 40%. ¿Cuál es la probabilidad experimental de sacar cualquier número que no sea 3 en este caso? Bueno, es simplemente una cuestión de restar 4 de 10, para obtener 6 de 10, o 60%.

Probemos con otro ejemplo. ¿Qué pasa si tiro el dado 30 veces y obtengo el número 6 un total de 10 veces? Entonces, ¿cuál es la probabilidad experimental de sacar un 6? Son 10 de 30, o 1/3. Ahora, saquemos una baraja estándar de 52 cartas. Si reemplazo cada carta después de cada intento y reorganizo el mazo después de cada intento, entonces si de cada diez intentos saco un corazón 5 veces, ¿cuál es la probabilidad experimental de que saque un corazón? Es 5 de 10 que es lo mismo que 1/2. 0,5 y 50%.

Las probabilidades experimentales no solo tienen que tratar solo con monedas, dados y cartas. Podemos aplicar este concepto a un escenario del mundo real.

Digamos que eres cajero en una tienda. Observas que de las 20 personas que han pasado por tu registro, 3 han comprado manzanas. ¿Cuál es la probabilidad experimental de que la próxima persona que vea compre manzanas? Son 3 de 20.

Si está parado en una intersección, simplemente mirando el tráfico pasar, y observa que de cada 100 autos, 3 son de color amarillo, entonces ¿cuál es la probabilidad experimental de que el próximo automóvil que vea sea de color amarillo? 3 de cada 100, o 3%.

Resumen de la lección

La probabilidad experimental es la relación entre el número de veces que ocurre un resultado y el número total de veces que se realiza la actividad. Ahora ha aprendido a aplicar este concepto a todo, desde lanzamientos de monedas hasta escenarios del mundo real. No olvide que la probabilidad experimental no es lo mismo que la probabilidad teórica. ¡Puede que no coincidan!

Articulos relacionados

• ¿Cuál es la medida de un ángulo agudo?
• Dimensionamiento y Tolerancia Geométricos: símbolos y diseño
• Actividades del teorema de la bisectriz de ángulo
• Plan de lección de medición de ángulos
• Juegos de volumen de un cilindro
• Poliedros: definición y tipos
• Apotema: definición y fórmula
• Lección de prisma para niños: definición y hechos
• Relación antisimétrica: definición, prueba y ejemplos
• Construcción de una línea paralela usando un punto que no está en la línea dada

• Probabilidad Empírica / Probabilidad Experimental: Definición Simple

Contenido de este artículo

• 1 ¿Qué es la probabilidad empírica?
• 2 Fórmula de probabilidad empírica
• 3 Frecuencia Experimental vs Empírica vs Relativa
• 4 Otros tipos de probabilidad
• 5 Referencia
• 6 Redactor del artículo
• 7 ¿Te hemos ayudado?

Actualizado el 2 de junio de 2022, por Luis Benites.

La investigación empírica , de donde obtenemos probabilidades empíricas , es donde se lleva a cabo la experimentación «práctica». En otras palabras, obtienes tus resultados de la experiencia real en lugar de una teoría o creencia.

¿Qué es la probabilidad empírica?

Fórmula de probabilidad empírica.

Fórmula de probabilidad experimental : número de formas en que ocurre la cosa / número de formas en que la cosa podría ocurrir.

Por ejemplo, supongamos que desea saber la probabilidad de que una persona prefiera la cola A sobre la cola B. Su prueba de sabor de 100 personas revela que 75 personas prefieren la cola A. Su probabilidad es: Número de formas en que ocurre la cosa (75) / número de formas en que la cosa podría ocurrir (100) = 75/100 = 3/4 o 75%.

Como fórmula matemática, la probabilidad empírica se denota con notación prima (Thompson, 2005): P′(A) = n(A) / n Donde:

• n(A) es el número de veces que sucede el evento A,
• n es el número de intentos en el experimento.

Frecuencia Experimental vs Empírica vs Relativa

La probabilidad experimental o probabilidad empírica también se denomina a veces «frecuencia relativa», pero normalmente encontrará el término reservado para aplicaciones como la tabla de frecuencia relativa . Probablemente sea más exacto decir que la probabilidad experimental es el proceso experimental de calcular las probabilidades (incluidos los resultados), mientras que la frecuencia relativa se refiere solo a los resultados. Para aumentar la confusión, también puede ver probabilidad experimental llamada «a posteriori» o » frecuencia «, pero estos términos no se usan con mucha frecuencia.

Otros tipos de probabilidad

Hay otros dos tipos de probabilidad (aparte de la probabilidad experimental/probabilidad empírica y la probabilidad teórica). Ellos son:

• La probabilidad subjetiva es su creencia de que ocurrirá un evento en particular. No hay ciencia detrás de esto. Podría ser la sensación de que “este billete raspadito será ganador” o su corazonada de que cierto medicamento para el resfriado es mejor que otro. La probabilidad subjetiva puede volverse extremadamente confusa cuando la probabilidad de una persona difiere de la de los demás. Por ejemplo, es posible que tengas la sensación de que hoy hará sol, mientras que otra persona piensa que va a llover.
• La probabilidad axiomática es una teoría de probabilidad unificadora. Establece un conjunto de reglas que se aplican a todos los tipos de probabilidad anteriores. Por ejemplo, una regla de probabilidad axiomática es que las probabilidades siempre están entre cero y 100 por ciento (es decir, de 0 a 1).

Thompson (2005). Capítulo 4: Probabilidad. ¿Qué es la probabilidad? Universidad de Texas .

Redactor del artículo

Tengo una Maestría en Ciencias en Estadística Aplicada y he trabajado en algoritmos de aprendizaje automático para empresas profesionales tanto en el sector de la salud como en el comercio minorista.

¿Te hemos ayudado?

Artículos relacionados:.

• Simulación Monte Carlo / Método
• Ley de Benford (la ley del primer dígito): definición simple, ejemplos
• Probabilidades de raspar: cómo aumentar su probabilidad de ganar
• Probabilidad posterior y distribución posterior
• Probabilidad Previa: Uniformativa, Conjugada

Deja un comentario Cancelar la respuesta

Guarda mi nombre, correo electrónico y web en este navegador para la próxima vez que comente.

Compartimos información EXCLUSIVA y GRATUITA solo para suscriptores (cursos privados, programas, consejos y mucho más)

You have Successfully Subscribed!

© 2013-2023 Enciclopedia Concepto. Todos los derechos reservados.

Probabilidad

Te explicamos qué es la probabilidad, sus tipos, ejemplos y la fórmula para calcularla. Además, las áreas en las que puede aplicarse.

¿Qué es la probabilidad?

El término probabilidad proviene de lo probable , o sea, de aquello que es más posible que ocurra, y se entiende como el mayor o menor grado de posibilidad de que un evento aleatorio ocurra , expresado en una cifra entre 1 (posibilidad total) y 0 (imposibilidad absoluta), o bien en porcentajes entre el 100% o el 0%, respectivamente.

Para obtener la probabilidad de un suceso, generalmente se determina la frecuencia con la que ocurre (en experimentos aleatorios bajo condiciones estables), y se procede a realizar cálculos teóricos.

Para ello se sigue lo establecido por la Teoría de la probabilidad, una rama de las matemáticas dedicada al estudio de la probabilidad. Esta disciplina es largamente empleada por otras ciencias naturales y sociales como disciplina auxiliar , ya que les permite manejar escenarios posibles en base a generalizaciones.

El origen de la probabilidad reside en la necesidad del ser humano de anticiparse a los hechos , y de predecir en cierta medida el futuro. Así, en su empeño por percibir patrones y conexiones en la realidad, se enfrentó constantemente al azar, o sea, a lo que carece de orden.

Las primeras consideraciones formales sobre esta materia provienen del siglo XVII, específicamente de la correspondencia entre Pierre de Fermat y Blaise Pascal en 1654, o de los estudios de Christiaan Huygens en 1657 y de la Kybeia de Juan Caramuel en 1649, texto hoy en día perdido.

Puede servirte: Polígono de frecuencias

Tipos de probabilidad

Existen los siguientes tipos de probabilidad:

• Frecuencial. Aquella que determina la cantidad de veces que un fenómeno puede ocurrir, considerando un número determinado de oportunidades, a través de la experimentación.
• Matemática . Pertenece al ámbito de la aritmética, y aspira al cálculo en cifras de la probabilidad de que determinados eventos aleatorios tengan lugar, a partir de la lógica formal y no de su experimentación.
• Binomial. Aquella en la que se estudia el éxito o fracaso de un evento, o cualquier otro tipo de escenario probable que tenga dos posibles resultados únicamente.
• Objetiva. Se denomina así a toda probabilidad en la que conocemos de antemano la frecuencia de un evento, y simplemente se dan a conocer los casos probables de que ocurra dicho evento.
• Subjetiva. Contrapuesta a la matemática, se sustenta en ciertas eventualidades que permiten inferir la probabilidad de un evento, aunque alejada de una probabilidad certera o calculable. De allí su subjetividad.
• Hipergeométrica. Aquella que se obtiene gracias a técnicas de muestreo, creando grupos de eventos según su aparición.
• Lógica. La que posee como rasgo característico que establece la posibilidad de ocurrencia de un hecho a partir de las leyes de la lógica inductiva.
• Condicionada. Aquella que se emplea para comprender la causalidad entre dos hechos distintos, cuando puede determinarse la ocurrencia de uno tras la ocurrencia del otro.

Ejemplos de probabilidad

La probabilidad se halla continuamente a nuestro alrededor. Los ejemplos más obvios de ella tienen que ver con juegos de azar : los dados, por ejemplo. Es posible determinar la frecuencia de aparición de cada cara, a partir de una serie continua de lanzamientos del dado. O también puede hacerse con la lotería, aunque ello exige cálculos tan enormes que, virtualmente, los hace imposibles de predecir.

También lidiamos con la probabilidad cuando consultamos el pronóstico del tiempo , y se nos advierte un cierto porcentaje de probabilidad de lluvia. Dependiendo de la cifra, será más o menos probable que llueva, pero podría ocurrir que no suceda, dado que se trata de una predicción, no de una certeza.

Fórmula para calcular la probabilidad

El cálculo de las probabilidades se lleva a cabo según la fórmula siguiente:

Probabilidad = Casos favorables / casos posibles x 100 (para llevarlo a porcentaje)

Así, por ejemplo, podemos calcular la probabilidad de que una moneda salga cara en un único lanzamiento, pensando que sólo puede salir una cara (1) de las dos que hay (2), esto es, 1 / 2 x 100 = 50% de probabilidad.

En cambio, si decidimos calcular cuántas veces saldrá la misma cara en dos lanzamientos seguidos, deberemos pensar que el caso favorable (cara y cara o sello y sello) es uno entre cuatro posibilidades de resultado (cara y cara, cara y sello, sello y cara, sello y sello). Por ende, 1 / 4 x 100 = 25% de probabilidad.

Aplicaciones de la probabilidad

El cálculo de la probabilidad tiene numerosas aplicaciones en la vida cotidiana, como son:

• El análisis de riesgo empresarial.  Según el cual se estiman las posibilidades de caída de precio de las acciones bursátiles, y se intenta predecir la conveniencia o no de la inversión en una u otra empresa.
• El análisis estadístico de la conducta.  De importancia para la sociología , emplea la probabilidad para evaluar la posible conducta de la población , y así predecir tendencias de pensamiento o de opinión. Es común verlo en las campañas electorales.
• La determinación de garantías y seguros.  Procesos en los que se evalúa la probabilidad de avería de los productos o la fiabilidad de un servicio (o de un asegurado, por ejemplo), para así saber cuánto tiempo de garantía conviene ofrecer, o a quiénes conviene asegurar y por cuánto.
• En la ubicación de partículas subatómicas .  Según el Principio de Incertidumbre de Heisenberg, el cual establece que no podemos saber dónde está una partícula subatómica en un momento determinado y al mismo tiempo a qué velocidad se mueve, de modo que los cálculos en la materia se realizan normalmente en términos probabilísticos: existe X por ciento de probabilidades de que la partícula esté allí.
• En la investigación biomédica.  Se calculan porcentajes de éxito y de fracaso de las drogas médicas o de las vacunas, para así saber si son fiables o no, y si conviene o no producirlas en masa, o a qué porcentaje de la población podrán causarle determinados efectos secundarios.

Sigue con: Estadística inferencial

Referencias

• “Probabilidad” en Wikipedia .
• “¿Qué es la probabilidad?” (video) en Math4all .
• “Probabilidad: conceptos básicos” en Khan Academy Español .
• “Probabilidad” en Sociedad Andaluza de Educación Matemática Thales (España).
• “Basic Probability” en Brown University (EEUU).
• “Probability Theory (Mathematics)” en The Encyclopaedia Britannica .

¿Te interesan nuestros contenidos?

Sigue nuestra cuenta de Instagram , donde publicamos contenidos exclusivos.

¿Te fue útil esta información?

¿Encontraste algún error? Envíanos tus comentarios y sugerencias.

¡Genial! Gracias por visitarnos :)

Síguenos en las redes:

etece.enciclopedias

• Matemáticas

Probabilidad

La probabilidad es el número de posibilidades que existen de que ocurra un evento particular.

Esta cifra es el resultado de un cálculo numérico. Se expresa normalmente mediante números enteros (es habitual utilizar cifras del 1 al 10) o porcentuales (que tienen como denominador común el número 100).

Por ejemplo, si lanzamos un dado de seis cifras, podemos decir que existe 1 posibilidad entre 6 de que salga el número 5. Pero también podríamos decir que existe un 16,6% de posibilidades de que saquemos un 5 (el resultado de dividir 100 entre 6).

La ciencia que mide y estudia las probabilidades es la estadística .

Los eventos sobre los que podemos determinar probabilidades son de cualquier condición. Por ello, la probabilidad puede ser utilizada en prácticamente todos los campos de la vida. Pero algunos, por su propia naturaleza, son más susceptibles de convertirse en objeto de la estadística. Entre ellos están el juego, los fenómenos meteorológicos, los resultados de una elección, etc.

Además, existen eventos cuya probabilidad de acontecer se puede cuantificar con más facilidad.

Las fórmulas para calcular la probabilidad son varias y dependen del evento y del tipo de probabilidad que necesitamos conocer. Estos son los principales:

• Frecuencial
• Condicional

Tipos de probabilidad

Probabilidad clásica o matemática.

Es el resultado de dividir el número de casos favorables (número de veces en que se produce un evento) entre el número total de casos posibles. Se trata de un cálculo teórico, basado en la lógica matemática y no en la experiencia.

Por ello, se ajusta muy bien a eventos o situaciones cuyo número de posibilidades es fácilmente calculable, como la tirada de un dado, la elección de una carta dentro de una baraja, etc.

Es conocida como probabilidad a priori o probabilidad lógica.

La fórmula básica para calcularla es:

Entendiendo por P (Probabilidad), por S, el número de casos favorables y por N, el número total de casos posibles.

Con esta fórmula podemos calcular la probabilidad de que salga el número que hemos elegido en la ruleta francesa (que consta de 37 números), utilizando esta misma fórmula.

Ver también Estadística

Probabilidad frecuencial

También se conoce como frecuentista y se basa en la frecuencia relativa con la que un evento ocurre en realidad (empíricamente). Es decir, la proporción de veces que sucede dentro de una serie de repeticiones idénticas o similares.

Por tanto, se considera que un evento es "probable" si tiende a ocurrir con cierta regularidad a medida que se repite el experimento muchas veces.

Se trata de un tipo de probabilidad que solo puede medirse si se dan las condiciones necesarias para realizarlo. Esto es que en el experimento se puedan controlar todas las variables y observar cómo se desarrollan los resultados en un gran número de repeticiones.

Podemos hacer uso de la probabilidad frecuencial a la hora de conocer la probabilidad de lluvia en un lugar determinado en un momento determinado del año. Para lo cual se deben haber medido todas las precipitaciones ocurridas año tras año en la misma fecha en el mismo lugar.

Probabilidad subjetiva

La probabilidad subjetiva es la que se calcula mediante fórmulas o experimentos, pero incluye también elementos basados en la opinión o juicio personal de quien realiza el experimento. Esto se produce porque, en ocasiones, existen elementos no cuantificables que pueden interferir en la probabilidad de que un evento suceda.

A diferencia de las interpretaciones frecuentistas o matemáticas, que se basan en observaciones empíricas o en cálculos formales, la probabilidad subjetiva refleja la incertidumbre percibida por una persona en función de su conocimiento y experiencia propios.

Podríamos usar la probabilidad subjetiva si quisiéramos medir las posibilidades de que un jugador de baloncesto enceste desde un punto x del campo de juego.

Para ello podríamos utilizar un experimento de probabilidad frecuencial, pero considerar que a medida que el jugador realiza el experimento gana en habilidad. Por tanto, podríamos "inferir" o "presuponer" que cuántas más veces realicemos el experimento, más aumentará la probabilidad de encestar del jugador.

Probabilidad conjunta

Mide la probabilidad de que dos eventos sucedan de forma simultánea. Es decir, que sucedan al mismo tiempo.

En el contexto de dos eventos (X, Y), la probabilidad conjunta se mediría mediante la siguiente fórmula.

Fórmula y ejemplo:

Con esta función podríamos medir, por ejemplo, las posibilidades de que al tirar una moneda al aire y un dado de 6 el resultado fuera cara y 6 al mismo tiempo.

Siendo X las posibilidades de que salga una cara de un dado e Y las posibilidades de que salga cara o cruz en una moneda:

Lo que equivale a un 8,33 % de posibilidades de que los dos eventos sucedan simultáneamente.

Probabilidad marginal

Es el cálculo de las posibilidades que existen de que aparezca un subconjunto de elementos determinado dentro de un conjunto más grande.

La probabilidad marginal permite calcular la probabilidad de un evento en una variable particular sin tener en cuenta las posibles combinaciones de valores de otras variables. Esto puede ser especialmente relevante cuando el objetivo es conocer las probabilidad estadística de una variable específica, sin necesidad de analizar la probabilidad de otras similares.

Ejemplo y fórmula para calcularla

La fórmula general para la probabilidad marginal de un evento x se calcula mediante la suma de las veces que se ha producido dicho evento dividido entre el número total de datos..

Por ejemplo, si se anota si ha habido personas mareadas durante la travesía de un barco, dependiendo del tiempo que ha hecho ese día durante treinta días, tendríamos:

• Días con personas mareadas con sol: 3
• Días con personas mareadas con lluvia: 9
• Días con personas no mareadas con sol: 11
• Días con personas no mareadas con lluvia: 7

Por lo tanto, cuatro de cada diez días habrá alguna persona mareada.

Probabilidad condicionada

La probabilidad condicionada o condicional mide las posibilidades que existen de que ocurra un evento, una vez que otro ya ha sucedido.

Se basa en la idea de que estamos restringiendo el espacio muestral al evento X. En el nuevo espacio muestral que consideramos, evaluamos la probabilidad de Y, en relación con las posibilidades dentro de ese espacio muestral reducido.

Fórmula y ejemplos

La fórmula matemática es:.

Por ejemplo , si al 30% de los miembros de tu familia les gusta jugar al tenis y al fútbol, y al 50% les gusta jugar al fútbol. ¿Qué probabilidades hay de que a un miembro de tu familia al que le guste jugar al fútbol le guste también el tenis?

Por tanto, la probabilidad de que a un miembro de tu familia le guste también el tenis es del 60%.

Probabilidad bayesiana

Se basa en la regla de Bayes y mide la probabilidad de una hipótesis en función de una nueva hipotesis dada. Es una forma de razonamiento probabilístico que nos permite ajustar la probabilidad de un hecho en función de la aparición de otro nuevo.

La fórmula clave en la probabilidad bayesiana es la regla de Bayes:

• P(X/Y) es la probabilidad de que suceda X habiendo sucedido Y.
• P(Y/X) es la probabilidad de que suceda Y habiendo sucedido X.
• P(X) es la probabilidad de que suceda X.
• P(Y) es la probabilidad de que suceda Y.

Por ejemplo , en una clase hay un 25% de posibilidades de que a un alumno le guste el Quijote, y un 30% de que les guste La Celestina. También se conoce el dato de que si a un alumno le gusta la Celestina, la posibilidad de que le guste El Quijote es del 50%.

La probabilidad bayesiana nos ayuda a saber el porcentaje de posibilidades de que a un alumno que le guste El Quijote le guste La Celestina.

• P(X/Y) es la probabilidad de que te guste el Quijote si te gusta La Celestina.
• P(Y/X) es la probabilidad de que te guste La Celestina si te gusta El Quijote.
• P(X) es la probabilidad de que te guste El Quijote.
• P(Y) es la probabilidad de que te guste La Celestina.

Por tanto, la probabilidad de que a un alumno le guste El Quijote habiéndole gustado La Celestina es del 41%.

Probabilidad geométrica

Permite conocer la probabilidad de que un elemento se encuentre en un punto determinado de un espacio dado.

Se mide dividiendo la longitud del segmento que buscamos conocer entre la longitud total del espacio.

Fórmula y ejemplo

Dado un segmento de 10 cm. de longitud, siendo A y C sus extremos y B un punto en esa línea. La distancia entre A y B es de 3 centímetros. Si necesitamos calcular la probabilidad de que un punto esté en la parte del segmento AB, la probabilidad será la longitud de esa parte del segmento dividida por la longitud total del segmento.

La probabilidad de que el punto esté en la parte del segmento AB es del 30%.

Cómo citar: Significados, Equipo (10/09/2024). "Probabilidad". En: Significados.com . Disponible en: https://www.significados.com/probabilidad/ Consultado:

• Estadística
• Complejidad
• Qué son las Matemáticas
• Tipos de triángulos
• Tipos de ángulos (sus nombres y medidas)
• Desviación estándar
• Ejemplos de estadística descriptiva para entender los conceptos básicos

Ciencia, Educación, Cultura y Estilo de Vida

Probabilidad

Explicamos qué es la probabilidad, los tipos que hay, cómo se calcula, ejemplos sencillos y sus aplicaciones

¿Qué es la probabilidad?

La probabilidad , matemáticamente hablando, de que ocurra un determinado evento es la medida en que dicho evento es predecible. Por ejemplo, si está nublado, es frecuente preguntarse ¿Cuál es la probabilidad de que llueva?

Dar la respuesta a esta pregunta mediante un valor numérico no es fácil, porque depende de muchísimos factores. Sin embargo una persona experta que se haya dedicado a estudiar minuciosamente el clima puede estimar, desde su experiencia, la probabilidad de que llueva si el día está nublado.

Es un tanto diferente cuando se trata de eventos con menos condicionantes, como el lanzamiento de una moneda honesta, que es aquella en la cual la probabilidad de que salga cualquiera de sus caras es la misma.

En este experimento solo hay dos alternativas de resultado: cara o sello, entonces, en una moneda honesta, la probabilidad de que salga cara es ½ y la probabilidad de que salga sello también es ½.

Las probabilidades son distintas en un dado, que es un cubo con seis caras numeradas del 1 al 6. La probabilidad de obtener un 3 en un solo lanzamiento se calcula fácilmente: es 1/6. Sin embargo, esta técnica no se aplica al cálculo de la probabilidad de lluvia, para el cual hace falta otro enfoque distinto, ya que son diferentes tipos de probabilidad.

La teoría de las probabilidades es una rama de las Matemáticas que tiene su origen en los juegos de azar, un entretenimiento muy popular entre las personas de todas las épocas. Hay evidencia arqueológica que muestra que hace 40.000 años o incluso más, ya los humanos empleaban dados para pasar el rato, así como en ceremonias religiosas.

Tipos de probabilidad

Está claro que existen diferentes interpretaciones de la probabilidad de acuerdo a la situación. De esta manera se tienen las probabilidades:

Probabilidad frecuentista

Para calcularla es preciso llevar a cabo una gran cantidad de experimentos y registrar la frecuencia con la que un evento determinado ocurre, llamada frecuencia absoluta. La probabilidad es la frecuencia relativa o cociente entre la cantidad de veces que el evento aparece y el número total de experimentos realizados.

Este tipo de probabilidad también recibe el nombre de probabilidad a posteriori .

Probabilidad clásica

Si un evento puede ocurrir de n formas diferentes, igualmente probables y excluyentes (quiere decir que si ocurre de una forma, no puede ocurrir de otra), la probabilidad clásica es el cociente entre el número de casos favorables al evento en cuestión y el total de casos posibles.

A este tipo de probabilidad se la conoce como probabilidad a priori .

Probabilidad objetiva

Probabilidad que se calcula mediante un criterio previamente establecido, el cual es independiente de la opinión del analista. La probabilidad objetiva puede ser a su vez teórica o experimental.

Probabilidad t eórica

Su valor se determina partiendo del razonamiento y conociendo todas las posibilidades en las que un evento puede ocurrir, suponiendo que todas ellas son igualmente probables.

Probabilidad e xperimental

Se calcula mediante el registro que se tiene de un experimento en particular y sus resultados. El experimento se lleva a cabo un determinado número de veces n , y un evento, de entre los varios que pueden ocurrir, aparece m veces. Por lo tanto, la probabilidad de ocurrencia de dicho evento es el cociente m/n .

Probabilidad s ubjetiva

Probabilidad que se calcula según la intuición o certidumbre que se tenga acerca de si el evento sucede o no. La certidumbre se obtiene gracias a la información disponible sobre el hecho, en conjunto con la experiencia del analista.

Probabilidad c ondicional

La probabilidad de que ocurra un suceso puede depender de la ocurrencia previa de un primer evento. En este caso la probabilidad del suceso está condicionada por la probabilidad del primero, y se dice que son sucesos dependientes.

Si por el contrario, la probabilidad de un evento no depende de la ocurrencia de otro, se trata de un evento independiente.

Probabilidad g eométrica

Se refiere a la probabilidad de que cierto punto se encuentre en una determinada región, ya sea de una línea, del plano o del espacio.

Probabilidad b inomial

Es la probabilidad asociada a una distribución binomial, que permite calcular la probabilidad de ocurrencia de un evento con dos resultados posibles, luego de llevar a cabo un cierto número n de experimentos independientes (el resultado anterior no afecta al siguiente).

El lanzamiento de una moneda es un evento con dos alternativas: cara o sello, también lo es el lanzar un dado y que el resultado sea par o impar.

Probabilidad h ipergeométrica

Es la probabilidad de aparición de una cualidad deseada, calculada a través de la distribución hipergeométrica. A través de esta distribución se puede caracterizar una población de tamaño N a través de una muestra de tamaño n, más pequeña, que se extrae de ella.

En dicha muestra, hay una cantidad C de elementos que poseen la cualidad deseada y x es la cantidad de veces que se selecciona un elemento con la cualidad.

Probabilidad m atemática

Consiste en el cálculo aritmético de la probabilidad de un evento aleatorio (un evento que ocurre al azar), siguiendo únicamente principios de lógica formal.

Probabilidad l ógica

Es la probabilidad que asigna a un evento mediante el uso de la lógica.

Ejemplos de probabilidad

La probabilidad siempre está comprendida entre 0 y 1, siendo posibles sucesos con probabilidad 0 y con probabilidad 1, tal como se ilustra seguidamente:

Suceso imposible

La probabilidad de un suceso imposible es 0, como obtener un 8 en el lanzamiento de un solo dado.

Suceso cierto

Un evento que siempre ocurre, pase lo que pase, tiene probabilidad igual a 1. Un ejemplo es obtener entre 1 y 6 puntos al lanzar un dado.

De un grupo de 80 estudiantes de la Facultad de Ciencias, 18 estudian física, 24 estudian matemática y 38 química. La probabilidad de que un estudiante seleccionado al azar estudie matemática es de 24/80 = 0.3 o 30%.

Obtener cara en el lanzamiento de una moneda

Una moneda tiene dos caras, y suponiendo que al lanzarla no quedará sobre el borde estrecho, caerá con la cara o el sello hacia arriba. Cualquiera de las dos posibilidades es igualmente probable, por lo que la probabilidad de obtener una cara es igual a la de obtener un sello: ½.

Probabilidad subjetiva

Si el día está muy nublado, al observarlo una persona estima que hay una probabilidad del 75% de que llueva, lo cual es una probabilidad subjetiva, basada en la experiencia del observador.

¿Cómo calcular la probabilidad?

Las siguientes son algunas formas de calcular la probabilidad de eventos:

Regla de Laplace

Para calcular la probabilidad clásica se emplea la regla de Laplace:

Probabilidad frecuencial

Al realizar un número grande de experimentos, la probabilidad de que ocurra el evento A se calcula como:

Aplicaciones de la probabilidad

La teoría de las probabilidades tiene numerosas aplicaciones en la práctica, como herramienta en la toma de decisiones:

Pólizas de seguros

Para asignar el valor de una póliza de seguros, ya sea de seguros o de automóviles, se divide a la población en categorías por edades y antecedentes, ya que cada categoría tiene diferente probabilidad de sufrir determinados percances. Por ejemplo, hay grupos con más riesgo de sufrir accidentes por choques de autos, o de tener un ataque cardíaco.

Control de calidad

Interesa saber qué probabilidades hay de encontrar piezas defectuosas en un lote, con  la finalidad de tomar medidas para mejorar la calidad del producto y ofrecer la garantía adecuada.

Mercado petrolero

La probabilidad de conflictos que involucran a países productores de determinadas materias primas estratégicas como el petróleo , inciden notablemente en los precios de este y sus derivados, como la gasolina.

Referencias

• Byju´s. Probability. Recuperado de: byjus.com.
• Clasificación De. Tipos de probabilidad. Recuperado de: clasificacionde.org.
• Mordecki, E. Probabilidad. Recuperado de: cmat.edu.uy.
• Triola, M. 2010. Elementary Statistics. 11th. Edition. Addison Wesley.
•  Lipschutz, S. 1998. Probabilidad. Serie Schaum. McGraw Hill.

What do you think about us?

Fundamentos de Probabilidad y Experimentos Aleatorios

Concept map.

La probabilidad es una rama de las matemáticas que estudia la frecuencia de eventos aleatorios y su previsibilidad. Se analizan conceptos como espacio muestral, eventos simples y compuestos, y se utilizan herramientas como tablas de contingencia y diagramas de árbol para calcular probabilidades. La independencia y compatibilidad de eventos son claves en la teoría de la probabilidad, afectando el cálculo de eventos complejos en situaciones aleatorias.

Probabilidad

Definición de probabilidad.

La probabilidad es una disciplina matemática que analiza la frecuencia con la que se espera que ocurra un evento aleatorio

Experimentos aleatorios

Lanzamiento de una moneda

Un experimento aleatorio típico es el lanzamiento de una moneda, que tiene dos posibles resultados: cara o cruz

Espacio muestral

El conjunto de todos los posibles resultados de un experimento se denomina espacio muestral

Eventos simples y compuestos

Los eventos pueden ser simples si consisten en un único resultado, o compuestos si incluyen varios resultados

Categorización de experimentos

Experimentos deterministas y aleatorios

Los experimentos se categorizan como deterministas cuando su resultado es predecible con certeza, y como aleatorios cuando no lo es

Experimentos simples y compuestos

Un experimento simple implica una sola acción, mientras que un experimento compuesto se compone de múltiples experimentos simples

Operaciones con eventos

Unión y intersección de eventos.

Las operaciones con eventos permiten analizar la ocurrencia de eventos combinados, como la unión y la intersección

Incompatibilidad y compatibilidad de eventos

Eventos incompatibles y compatibles

Los eventos son incompatibles si no tienen resultados en común y son compatibles si pueden ocurrir juntos

Propiedades de las operaciones

Las propiedades de las operaciones, como la conmutativa, asociativa y distributiva, son esenciales para el cálculo de probabilidades

Resolución de problemas

Las propiedades de las operaciones facilitan la resolución de problemas complejos de manera estructurada y sistemática

Frecuencia y probabilidad

Frecuencia absoluta y relativa.

La frecuencia absoluta es el número de veces que un evento se presenta en un conjunto de pruebas, mientras que la frecuencia relativa es la proporción de la frecuencia absoluta respecto al número total de pruebas

Ley de los grandes números

Según la ley de los grandes números, las frecuencias relativas se estabilizan alrededor de la probabilidad teórica del evento a medida que el número de pruebas aumenta

Regla de Laplace

La regla de Laplace define la probabilidad de un evento como el cociente entre el número de casos favorables y el número total de casos posibles

Eventos compuestos y condicionales

Probabilidad de secuencias de eventos.

En experimentos compuestos, la probabilidad de ocurrencia de una secuencia de eventos se determina multiplicando las probabilidades de cada evento individual

Eventos independientes y dependientes

Si la ocurrencia de un evento afecta la probabilidad del otro, se consideran eventos dependientes

Probabilidad condicional

La probabilidad condicional es la probabilidad de que ocurra un evento dado que ya ocurrió otro evento

Herramientas para el cálculo de probabilidades

Tablas de contingencia.

Las tablas de contingencia facilitan la organización y el análisis de datos de eventos aleatorios y el cálculo de sus probabilidades

Diagramas de árbol

Los diagramas de árbol son representaciones gráficas que ilustran todas las posibles secuencias de eventos en un experimento compuesto, con sus respectivas probabilidades

Uso en eventos dependientes o condicionales

Estas herramientas son indispensables para entender eventos dependientes o condicionales y calcular probabilidades en experimentos con varias etapas

Want to create maps from your material?

Enter text, upload a photo, or audio to Algor. In a few seconds, Algorino will transform it into a conceptual map, summary, and much more!

Learn with Algor Education flashcards

Click on each card to learn more about the topic.

La ______ es una rama de las matemáticas que estudia la frecuencia de eventos que no tienen un resultado cierto.

probabilidad

El lanzamiento de una ______ es un ejemplo de un experimento aleatorio con dos resultados posibles: ______ o ______.

moneda cara cruz

Un evento se considera ______ si tiene una probabilidad de cero de suceder, y ______ si su probabilidad es uno.

imposible seguro

Eventos incompatibles

Eventos sin resultados comunes, no pueden ocurrir al mismo tiempo.

Eventos compatibles

Eventos con resultados comunes, pueden ocurrir simultáneamente.

Propiedades de operaciones en probabilidad

Conmutativa, asociativa, distributiva; fundamentales para cálculo de probabilidades.

La ______ ______ indica cuántas veces sucede algo en un grupo de intentos.

frecuencia absoluta

La probabilidad de que ocurra un suceso se mide en una escala de ______ a ______.

Conforme aumenta el número de intentos, las frecuencias relativas tienden a aproximarse a la probabilidad ______ del suceso.

La ______ de ______ es una fórmula para calcular la probabilidad cuando todos los resultados son igualmente posibles.

regla Laplace

Eventos independientes en probabilidad

Eventos que no se afectan entre sí; la ocurrencia de uno no altera la probabilidad del otro.

Eventos dependientes en probabilidad

Eventos cuya ocurrencia afecta la probabilidad del otro; no son independientes.

Cálculo de probabilidad condicional

P(B | A) se calcula dividiendo la probabilidad de la intersección de A y B por la probabilidad de A.

Los ______ de árbol son representaciones que muestran todas las posibles secuencias de eventos y sus ______ en experimentos compuestos.

diagramas probabilidades

Definición de eventos incompatibles

Eventos que no pueden ocurrir al mismo tiempo.

Definición de eventos independientes

La ocurrencia de un evento no afecta la probabilidad del otro.

Verificación de independencia de eventos

Dos eventos son independientes si el producto de sus probabilidades es igual a la probabilidad de que ambos sucedan juntos.

Here's a list of frequently asked questions on this topic

¿qué es un experimento aleatorio y cómo se clasifican los eventos dentro de su espacio muestral, ¿qué significan la unión e intersección de eventos en el contexto de la probabilidad, ¿cómo se relacionan la frecuencia absoluta y relativa con la probabilidad de un evento, ¿cómo se calcula la probabilidad de eventos compuestos y la probabilidad condicional, ¿cuál es la utilidad de las tablas de contingencia y los diagramas de árbol en probabilidad, ¿en qué se diferencian los eventos incompatibles de los independientes, similar contents, explore other maps on similar topics.

Fundamentos de la Distribución Binomial

Medidas de Dispersión y Tendencia Central en Estadística

Introducción al Cálculo Integral

Teoría de Conjuntos

Conceptos Fundamentales de la Derivación

Conceptos Fundamentales de los Polinomios

Conceptos Fundamentales de Factorización

Can't find what you were looking for?

Search for a topic by entering a phrase or keyword

Operaciones con Eventos y sus Propiedades en Probabilidad

Relación entre frecuencia y probabilidad, probabilidad de eventos compuestos y condicionales, utilización de tablas de contingencia y diagramas de árbol, diferenciación entre independencia y compatibilidad de eventos.

Edit available

Experimento (probabilidad)

Un experimento en teoría de la probabilidad y estadística , es un proceso controlado que proporciona datos sobre un conjunto de posibles resultados . Estos resultados pueden conocerse previamente o no, y pueden ser numéricos o no numéricos. Al rango del conjunto de todos los posibles resultados se denomina espacio muestral . Los experimentos se caracterizan porque pueden repetirse infinitamente, y porque sus resultados son medibles. En probabilidad, existen dos grandes categorías de experimentos: aleatorios y deterministas.

Un experimento aleatorio es aquel que al repetirse con las mismas condiciones iniciales no garantiza los mismos resultados. Es decir, las condiciones del experimento no determinan los resultados. Por ejemplo, al lanzar una moneda no se conoce si saldrá cara o cruz, o al lanzar un dado no se conoce qué número caerá. Por ello, los experimentos aleatorios admiten más de un posible resultado. Dentro de los experimentos aleatorios, aquellos que poseen exactamente dos resultados posibles (mutuamente excluyentes) se conocen como ensayo de Bernoulli .

Mientras que un experimento determinista (o determinístico) es aquel en donde existe certeza acerca del resultado que ocurrirá cuando éste sea repetido varias veces. Es decir, las condiciones del experimento determinan el resultado. Por ejemplo, enfriar agua por debajo de los 0º celsius. Por lo que los experimentos deterministas solo tiene un posible resultado.

Al realizar un experimento (cualquiera que sea), este finaliza con un resultado (y solo uno), aunque este resultado puede encajar dentro de varios eventos (grupos de resultados). En este contexto, se considera que todos esos eventos han ocurrido durante el ensayo. Mediante la repetición de un experimento se van acumulando los resultados obtenidos, lo cual permite a los investigadores calcular las probabilidades empíricas asociadas a resultados y eventos. Este proceso de repetición permite convertir el diseño metodológico en una distribución estadística.

Diferencia entre ensayo y experimento

Los experimentos aleatorios a menudo se realizan repetidamente, de modo que los resultados colectivos puedan someterse a un análisis estadístico. Un número fijo de repeticiones del mismo experimento puede considerarse como un experimento compuesto , en cuyo caso las repeticiones individuales se denominan ensayos . Por ejemplo, si uno lanzara la misma moneda cien veces y registrara cada resultado, cada lanzamiento se consideraría una prueba dentro del experimento compuesto por los cien lanzamientos.

Descripción matemática del experimento

Un experimento aleatorio se describe o modela mediante una construcción matemática conocida como espacio de probabilidad. Un espacio de probabilidad se construye y define con un tipo específico de experimento o ensayo en mente.

Una descripción matemática de un experimento consta de tres partes:

• Un espacio muestral, Ω (o S ), que es el conjunto de todos los resultados posibles.

• La asignación de probabilidades a los eventos, es decir, una función P que mapea de eventos a probabilidades.

Como experimento simple, podemos lanzar una moneda dos veces. El espacio muestral (donde el orden de los dos lanzamientos es relevante) es {(H, T), (T, H), (T, T), (H, H)} donde "H" significa "cara" y " T" significa "cruz". Tenga en cuenta que cada uno de (H, T), (T, H) ,... son posibles resultados del experimento. Podemos definir un evento que ocurre cuando ocurre "cara" en cualquiera de los dos lanzamientos. Este evento contiene todos los resultados excepto (T, T) .

Contenido relacionado

Ley de los grandes números

Unidad estadística

Valor esperado