Factoring Calculator
What do you want to calculate.
- Solve for Variable
- Practice Mode
- Step-By-Step

Example (Click to try)
How to factor expressions.
- Add up to 5
- Multiply together to get 4
Current calculator limitations
- Doesn't support multivariable expressions
- If you have an expression that you want the calculator to support in the future, please contact us
Factoring Expressions Video Lesson
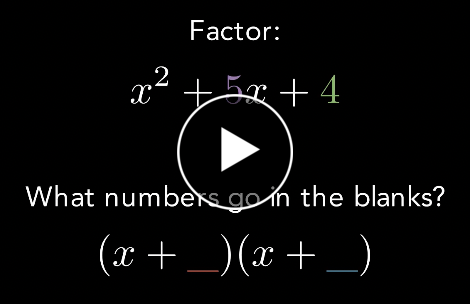
Need more problem types? Try MathPapa Algebra Calculator
Clear Factoring Calculator »

- Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
- Graphing Line Graph Calculator Exponential Graph Calculator Quadratic Graph Calculator Sine Graph Calculator More...
- Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
- Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
- Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
- Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
- Algebra Equations Inequalities System of Equations System of Inequalities Testing Solutions Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Prove That Logical Sets Word Problems
- Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Coterminal Angle Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
- Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
- Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
- Linear Algebra Matrices Vectors
- Trigonometry Quadrant Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
- Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
- Physics Mechanics
- Chemistry Chemical Reactions Chemical Properties
- Finance Simple Interest Compound Interest Present Value Future Value
- Economics Point of Diminishing Return
- Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Degrees Minutes Seconds Hexadecimal Scientific Notation Distance Weight Time Volume
- Pre Algebra
- One-Step Addition
- One-Step Subtraction
- One-Step Multiplication
- One-Step Division
- One-Step Decimals
- Two-Step Integers
- Two-Step Add/Subtract
- Two-Step Multiply/Divide
- Two-Step Fractions
- Two-Step Decimals
- Multi-Step Integers
- Multi-Step with Parentheses
- Multi-Step Rational
- Multi-Step Fractions
- Multi-Step Decimals
- Solve by Factoring
- Completing the Square
- Quadratic Formula
- Biquadratic
- Logarithmic
- Exponential
- Rational Roots
- Floor/Ceiling
- Equation Given Roots
- Equation Given Points
- Newton Raphson
- Substitution
- Elimination
- Cramer's Rule
- Gaussian Elimination
- System of Inequalities
- Testing Solutions
- Perfect Squares
- Difference of Squares
- Difference of Cubes
- Sum of Cubes
- Polynomials
- Factor Completely
- Distributive Property
- FOIL method
- Perfect Cubes
- Binomial Expansion
- Negative Rule
- Product Rule
- Quotient Rule
- Expand Power Rule
- Fraction Exponent
- Exponent Rules
- Exponential Form
- Logarithmic Form
- Absolute Value
- Rational Number
- Powers of i
- Complex Form
- Partial Fractions
- Is Polynomial
- Leading Coefficient
- Leading Term
- Standard Form
- Complete the Square
- Synthetic Division
- Ruffini Method
- Linear Factors
- Rationalize Denominator
- Rationalize Numerator
- Identify Type
- Convergence
- Interval Notation
- Pi (Product) Notation
- Boolean Algebra
- Truth Table
- Mutual Exclusive
- Cardinality
- Caretesian Product
- Age Problems
- Distance Problems
- Cost Problems
- Investment Problems
- Number Problems
- Percent Problems
- Addition/Subtraction
- Multiplication/Division
- Dice Problems
- Coin Problems
- Card Problems
- Pre Calculus
- Linear Algebra
- Trigonometry
- Conversions
Number Line
- factor\:x^{2}-5x+6
- factor\:(x-2)^2-9
- factor\:2x^2-18
- factor\:5a^2-30a+45
- factor\:x^6-2x^4-x^2+2
- factor\:2x^5+x^4-2x-1
- What is the sum of cubes formula?
- The sum of cubes formula is a³ + b³ = (a+b)(a² - ab + b²)
- What is the difference of squares formula?
- The difference of squares formula is a² - b² = (a+b)(a-b)
- What is the difference of cubes formula?
- The difference of cubes formula is a³ - b³ = (a-b)(a² + ab + b²)
- How do you solve factoring by greatest common monomial factor?
- To factor by greatest common monomial factor, find the greatest common monomial factor among the terms of the expression and then factor it out of each term.
- How do you factor a monomial?
- To factor a monomial, write it as the product of its factors and then divide each term by any common factors to obtain the fully-factored form.
- How do you factor a binomial?
- To factor a binomial, write it as the sum or difference of two squares or as the difference of two cubes.
- How do you factor a trinomial?
- To factor a trinomial x^2+bx+c find two numbers u, v that multiply to give c and add to b. Rewrite the trinomial as the product of two binomials (x-u)(x-v)
- How to find LCM with the listing multiples method?
- To find the LCM of two numbers using the listing multiples method write down the multiples of the first number and write down the multiples of the second number. Find the smallest number that is a multiple of both of the numbers.
factor-calculator
- Middle School Math Solutions – Polynomials Calculator, Factoring Quadratics Just like numbers have factors (2×3=6), expressions have factors ((x+2)(x+3)=x^2+5x+6). Factoring is the process...
We want your feedback
Please add a message.
Message received. Thanks for the feedback.
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
The process of factoring is essential to the simplification of many algebraic expressions and is a useful tool in solving higher degree equations. In fact, the process of factoring is so important that very little of algebra beyond this point can be accomplished without understanding it.
In earlier chapters the distinction between terms and factors has been stressed. You should remember that terms are added or subtracted and factors are multiplied. Three important definitions follow.
Terms occur in an indicated sum or difference. Factors occur in an indicated product.
- An expression is in factored form only if the entire expression is an indicated product.

Note in these examples that we must always regard the entire expression. Factors can be made up of terms and terms can contain factors, but factored form must conform to the definition above.
Factoring is a process of changing an expression from a sum or difference of terms to a product of factors.
Note that in this definition it is implied that the value of the expression is not changed - only its form.
REMOVING COMMON FACTORS
- Determine which factors are common to all terms in an expression.
- Factor common factors.
In the previous chapter we multiplied an expression such as 5(2x + 1) to obtain 10x + 5. In general, factoring will "undo" multiplication. Each term of 10x + 5 has 5 as a factor, and 10x + 5 = 5(2x + 1).
To factor an expression by removing common factors proceed as in example 1.
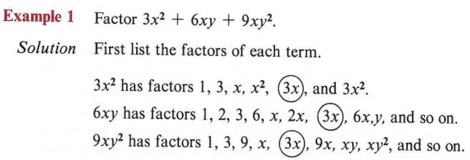
Next look for factors that are common to all terms, and search out the greatest of these. This is the greatest common factor. In this case, the greatest common factor is 3x.
Proceed by placing 3x before a set of parentheses.
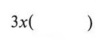
The terms within the parentheses are found by dividing each term of the original expression by 3x.
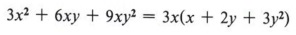
If we had only removed the factor "3" from 3x 2 + 6xy + 9xy 2 , the answer would be
3(x 2 + 2xy + 3xy 2 ).
Multiplying to check, we find the answer is actually equal to the original expression. However, the factor x is still present in all terms. Hence, the expression is not completely factored.
- It must be possible to multiply the factored expression and get the original expression.
- FThe expression must be completely factored.
Example 2 Factor 12x 3 + 6x 2 + 18x.
At this point it should not be necessary to list the factors of each term. You should be able to mentally determine the greatest common factor. A good procedure to follow is to think of the elements individually. In other words, don�t attempt to obtain all common factors at once but get first the number, then each letter involved. For instance, 6 is a factor of 12, 6, and 18, and x is a factor of each term. Hence 12x 3 + 6x 2 + 18x = 6x(2x 2 + x + 3). Multiplying, we get the original and can see that the terms within the parentheses have no other common factor, so we know the solution is correct.
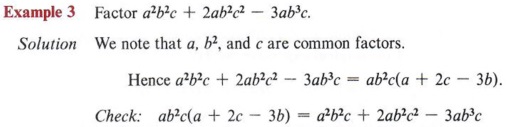
If an expression cannot be factored it is said to be prime .

FACTORING BY GROUPING
- Factor expressions when the common factor involves more than one term.
- Factor by grouping.
An extension of the ideas presented in the previous section applies to a method of factoring called grouping .
First we must note that a common factor does not need to be a single term. For instance, in the expression 2y(x + 3) + 5(x + 3) we have two terms. They are 2y(x + 3) and 5(x + 3). In each of these terms we have a factor (x + 3) that is made up of terms. This factor (x + 3) is a common factor.
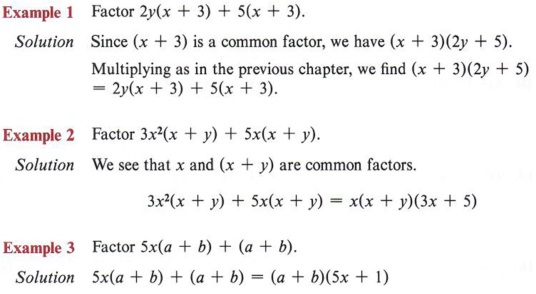
Sometimes when there are four or more terms, we must insert an intermediate step or two in order to factor.
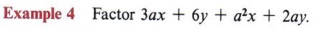
First note that not all four terms in the expression have a common factor, but that some of them do. For instance, we can factor 3 from the first two terms, giving 3(ax + 2y). If we factor a from the remaining two terms, we get a(ax + 2y). The expression is now 3(ax + 2y) + a(ax + 2y), and we have a common factor of (ax + 2y) and can factor as (ax + 2y)(3 + a). Multiplying (ax + 2y)(3 + a), we get the original expression 3ax + 6y + a 2 x + 2ay and see that the factoring is correct.
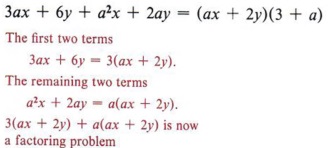
This is an example of factoring by grouping since we "grouped" the terms two at a time.
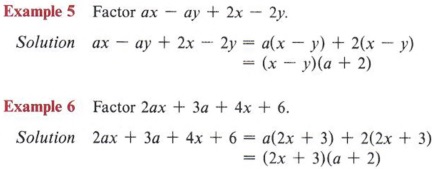
Sometimes the terms must first be rearranged before factoring by grouping can be accomplished.
Example 7 Factor 3ax + 2y + 3ay + 2x.
The first two terms have no common factor, but the first and third terms do, so we will rearrange the terms to place the third term after the first. Always look ahead to see the order in which the terms could be arranged.
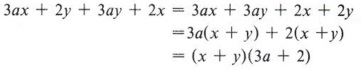
In all cases it is important to be sure that the factors within parentheses are exactly alike. This may require factoring a negative number or letter.
Example 8 Factor ax - ay - 2x + 2y.
Note that when we factor a from the first two terms, we get a(x - y). Looking at the last two terms, we see that factoring +2 would give 2(-x + y) but factoring "-2" gives - 2(x - y). We want the terms within parentheses to be (x - y), so we proceed in this manner.
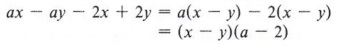
FACTORING TRINOMIALS
- Mentally multiply two binomials.
- Factor a trinomial having a first term coefficient of 1.
- Find the factors of any factorable trinomial.
A large number of future problems will involve factoring trinomials as products of two binomials. In the previous chapter you learned how to multiply polynomials. We now wish to look at the special case of multiplying two binomials and develop a pattern for this type of multiplication.
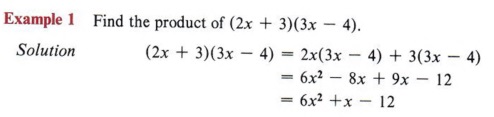
Since this type of multiplication is so common, it is helpful to be able to find the answer without going through so many steps. Let us look at a pattern for this.
From the example (2x + 3)(3x - 4) = 6x 2 + x - 12, note that the first term of the answer (6x 2 ) came from the product of the two first terms of the factors, that is (2x)(3x).
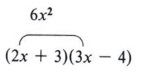
Also note that the third term (-12) came from the product of the second terms of the factors, that is ( + 3)(-4).
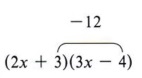
We now have the following part of the pattern:
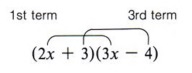
Now looking at the example again, we see that the middle term (+x) came from a sum of two products (2x)( -4) and (3)(3x).
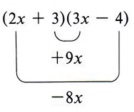
- First term by first term
- Outside terms
- Inside terms
- Last term by last term
These products are shown by this pattern.
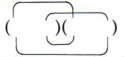
When the products of the outside terms and inside terms give like terms, they can be combined and the solution is a trinomial.
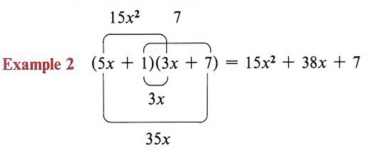
You should memorize this pattern.
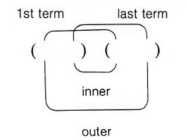
Not only should this pattern be memorized, but the student should also learn to go from problem to answer without any written steps. This mental process of multiplying is necessary if proficiency in factoring is to be attained.
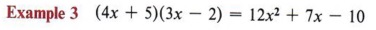
As you work the following exercises, attempt to arrive at a correct answer without writing anything except the answer. The more you practice this process, the better you will be at factoring.
Now that we have established the pattern of multiplying two binomials, we are ready to factor trinomials. We will first look at factoring only those trinomials with a first term coefficient of 1.
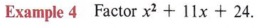
Since this is a trinomial and has no common factor we will use the multiplication pattern to factor.
First write parentheses under the problem.
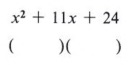
We now wish to fill in the terms so that the pattern will give the original trinomial when we multiply. The first term is easy since we know that (x)(x) = x 2 .
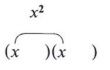
We must now find numbers that multiply to give 24 and at the same time add to give the middle term. Notice that in each of the following we will have the correct first and last term.
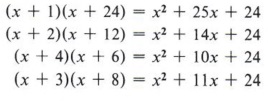
Only the last product has a middle term of 11x, and the correct solution is
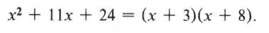
This method of factoring is called trial and error - for obvious reasons.
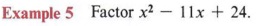
Here the problem is only slightly different. We must find numbers that multiply to give 24 and at the same time add to give - 11. You should always keep the pattern in mind. The last term is obtained strictly by multiplying, but the middle term comes finally from a sum. Knowing that the product of two negative numbers is positive, but the sum of two negative numbers is negative, we obtain
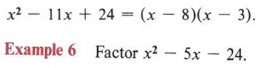
We are here faced with a negative number for the third term, and this makes the task slightly more difficult. Since -24 can only be the product of a positive number and a negative number, and since the middle term must come from the sum of these numbers, we must think in terms of a difference. We must find numbers whose product is 24 and that differ by 5. Furthermore, the larger number must be negative, because when we add a positive and negative number the answer will have the sign of the larger. Keeping all of this in mind, we obtain
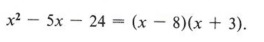
- When the sign of the third term is positive, both signs in the factors must be alike-and they must be like the sign of the middle term.
- When the sign of the last term is negative, the signs in the factors must be unlike-and the sign of the larger must be like the sign of the middle term.
In the previous exercise the coefficient of each of the first terms was 1. When the coefficient of the first term is not 1, the problem of factoring is much more complicated because the number of possibilities is greatly increased.

Notice that there are twelve ways to obtain the first and last terms, but only one has 17x as a middle term.

There is only one way to obtain all three terms:
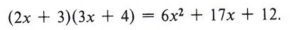
In this example one out of twelve possibilities is correct. Thus trial and error can be very time-consuming.
Even though the method used is one of guessing, it should be "educated guessing" in which we apply all of our knowledge about numbers and exercise a great deal of mental arithmetic. In the preceding example we would immediately dismiss many of the combinations. Since we are searching for 17x as a middle term, we would not attempt those possibilities that multiply 6 by 6, or 3 by 12, or 6 by 12, and so on, as those products will be larger than 17. Also, since 17 is odd, we know it is the sum of an even number and an odd number. All of these things help reduce the number of possibilities to try.
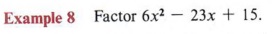
- The last term is positive, so two like signs.
- The middle term is negative, so both signs will be negative.
- The factors of 6x2 are x, 2x, 3x, 6x. The factors of 15 are 1, 3, 5, 15.
- Eliminate as too large the product of 15 with 2x, 3x, or 6x. Try some reasonable combinations.

- The last term is negative, so unlike signs.
- We must find products that differ by 5 with the larger number negative.
- We eliminate a product of 4x and 6 as probably too large.
- Try some combinations.
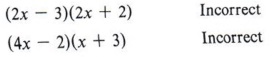
(4x - 3)(x + 2) : Here the middle term is + 5x, which is the right number but the wrong sign. Be careful not to accept this as the solution, but switch signs so the larger product agrees in sign with the middle term.

SPECIAL CASES IN FACTORING
- Identify and factor the differences of two perfect squares.
- Identify and factor a perfect square trinomial.
In this section we wish to examine some special cases of factoring that occur often in problems. If these special cases are recognized, the factoring is then greatly simplified.
The first special case we will discuss is the difference of two perfect squares .
Recall that in multiplying two binomials by the pattern, the middle term comes from the sum of two products.
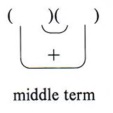
From our experience with numbers we know that the sum of two numbers is zero only if the two numbers are negatives of each other.
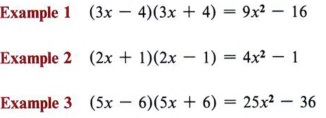
In each example the middle term is zero. Note that if two binomials multiply to give a binomial (middle term missing), they must be in the form of (a - b) (a + b).
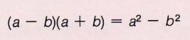
Here both terms are perfect squares and they are separated by a negative sign.
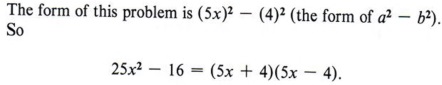
Special cases do make factoring easier, but be certain to recognize that a special case is just that-very special. In this case both terms must be perfect squares and the sign must be negative, hence "the difference of two perfect squares."

You must also be careful to recognize perfect squares. Remember that perfect square numbers are numbers that have square roots that are integers. Also, perfect square exponents are even.
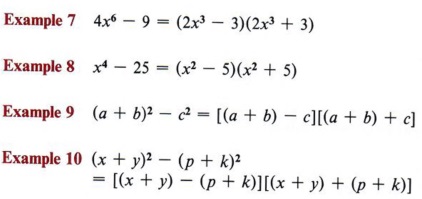
Another special case in factoring is the perfect square trinomial. Observe that squaring a binomial gives rise to this case.
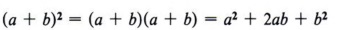
- The first term is a perfect square.
- The third term is a perfect square.
- The middle term is twice the product of the square root of the first and third terms.
- 25x 2 is a perfect square-principal square root = 5x.
- 4 is a perfect square-principal square root = 2.
- 20x is twice the product of the square roots of 25x 2 and
- 20x = 2(5x)(2).
To factor a perfect square trinomial form a binomial with the square root of the first term, the square root of the last term, and the sign of the middle term, and indicate the square of this binomial.
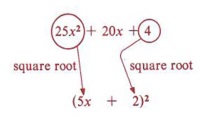
Thus, 25x 2 + 20x + 4 = (5x + 2) 2
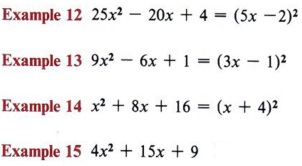
Not the special case of a perfect square trinomial.

OPTIONAL SHORTCUTS TO TRIAL AND ERROR FACTORING
- Find the key number of a trinomial.
- Use the key number to factor a trinomial.
In this section we wish to discuss some shortcuts to trial and error factoring. These are optional for two reasons. First, some might prefer to skip these techniques and simply use the trial and error method; second, these shortcuts are not always practical for large numbers. However, they will increase speed and accuracy for those who master them.
The first step in these shortcuts is finding the key number . After you have found the key number it can be used in more than one way.
In a trinomial to be factored the key number is the product of the coefficients of the first and third terms.

The first use of the key number is shown in example 3.
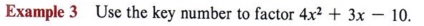
A second use for the key number as a shortcut involves factoring by grouping. It works as in example 5.
COMPLETE FACTORIZATION
- First look for common factors.
- Factor the remaining trinomial by applying the methods of this chapter.
We have now studied all of the usual methods of factoring found in elementary algebra. However, you must be aware that a single problem can require more than one of these methods. Remember that there are two checks for correct factoring.
- Will the factors multiply to give the original problem?
- Are all factors prime?

A good procedure to follow in factoring is to always remove the greatest common factor first and then factor what remains, if possible.
- Factoring is a process that changes a sum or difference of terms to a product of factors.
- A prime expression cannot be factored.
- The greatest common factor is the greatest factor common to all terms.
- An expression is completely factored when no further factoring is possible.
- The possibility of factoring by grouping exists when an expression contains four or more terms.
- The FOIL method can be used to multiply two binomials.
- Special cases in factoring include the difference of two squares and perfect square trinomials .
- The key number is the product of the coefficients of the first and third terms of a trinomial.
- To remove common factors find the greatest common factor and divide each term by it.
- To factor a perfect square trinomial form a binomial with the square root of the first term, the square root of the last term, and the sign of the middle term and indicate the square of this binomial.
- Use the key number as an aid in determining factors whose sum is the coefficient of the middle term of a trinomial.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions
Factoring by Common Factors & by Grouping
Related Pages More Factoring and Algebra Lessons Algebra Worksheets Algebra Games
In these lessons, we will look at factoring by common factors and factoring of polynomials by grouping.
The following diagram shows the steps to factor a polynomial with four terms using grouping. Scroll down the page for examples and solutions.

The following diagram shows the steps to factor a trinomial using grouping. Scroll down the page for examples and solutions.

Printable & Online Algebra Worksheets
Factoring By Common Factors
The first step in factorizing is to find and extract the GCF of all the terms.
Example: Factorize the following algebraic expressions: a) xyz – x 2 z b) 6a 2 b + 4bc
Solution: a) xyz – x 2 z = xz(y – x) b) 6a 2 b + 4bc = 2b(3a 2 + 2c)
Factoring Out The Greatest Common Factor Factoring is a technique that is useful when trying to solve polynomial equations algebraically. We begin by looking for the Greatest Common Factor (GCF) of a polynomial expression. The GCF is the largest monomial that divides (is a factor of) each term of of the polynomial. The following video shows an example of simple factoring or factoring by common factors. To find the GCF of a Polynomial
- Write each term in prime factored form
- Identify the factors common in all terms
- Factor out the GCF
Examples: Factor out the GCF
- 2x 4 - 16x 3
- 4x 2 y 3 + 20xy 2 + 12xy
- -2x 3 + 8x 2 - 4x
- -y 3 - 2y 2 + y - 7
Factoring Using the Great Common Factor, GCF - Example 1 Two examples of factoring out the greatest common factor to rewrite a polynomial expression.
Example: Factor out the GCF: a) 2x 3 y 8 + 6x 4 y 2 + 10x 5 y 10 b) 6a 10 b 8 + 3a 7 b 4 - 24a 5 b 6
Factoring Using the Great Common Factor, GCF - Example 2
Example: Factor out binomial expressions. a) 3x 2 (2x + 5y) + 7y 2 (2x + 5y) b) 5x 2 (x + 3y) - 15x 3 (x + 3y)
Factoring Polynomials with Common Factors This video provides examples of how to factor polynomials that require factoring out the GCF as the first step. Then other methods are used to completely factor the polynomial.
Example: Factor 4x 2 - 64 3x 2 + 3x - 36 2x 2 - 28x + 98
Factoring By Grouping
When an expression has an even number of terms and there are no common factors for all the terms, we may group the terms into pairs and find the common factor for each pair:
Example: Factorize the following expressions:
a) ax + ay + bx + by b) 2x + 8y – 3px –12py c) 3x – 3y + 4ay – 4ax
Solution: a) ax + ay + bx + by = a(x + y) + b(x + y) = (a + b)(x + y)
b) 2x + 8y – 3px –12py = 2(x + 4y) –3p(x + 4y) = (2 – 3p)(x + 4y)
c) 3x – 3y + 4ay – 4ax = 3(x – y) + 4a(y – x) = 3(x – y) – 4a(x – y) = (3 – 4a)( x – y)
How to Factor by Grouping? 3 complete examples of solving quadratic equations using factoring by grouping are shown.
- Factor x(x + 1) - 5(x + 1)
- Solve 2x 2 + 5x + 2 = 0
- Solve 7x 2 + 16x + 4 = 0
- Solve 6x 2 - 17x + 12 = 0
Factoring by Grouping - Ex 1
Example: Factor: a) 2x 2 + 7x 2 + 2x + 7 b) 10x 2 + 2xy + 15xy + 3y 2
Factoring By Grouping - Ex 2
Example: Factor: 12u 2 + 15uv + 24uv 2 + 30v 3
Factoring Trinomials: Factor by Grouping - ex 1
Example: Factor 12x 2 + 34x + 10
Factoring Trinomials: Factor by Grouping - ex 2
Example: Factor 6x 2 + 15x - 21
Factoring by grouping - Prime Factorization
Example: 12a 3 - 9a 2 b - 8ab 2 + 6b 3

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Factoring Algebraic Expressions Word Problems
Factorization of algebraic means finding the factors of the given expression which refers to finding two or more expressions whose product is the given expression. This process of finding two or more expressions whose product is the given expression is known as the factorization of algebraic expressions. A factor is a number that divides the given number without any remainder. It simply means expressing a number as a multiplication of two other numbers. Similarly, in Algebra we write the algebraic expressions as a product of their factors. The only difference here is that an algebraic expression involves numbers and variables combined with an arithmetic operation like addition or subtraction.
1. Read the word problem and determine the greatest common factor of the terms. 2. Keep the greatest common factor outside the brackets, divide the polynomial terms by this factor and write the remaining expression inside the brackets. 3. Verify your answer by multiplying the factors to get the original expression.
A rectangular garden is being separated into 6 equal sections for different types of flowers. The area of the garden is (12x + 30) square meters. What is the area of each section of the garden?
1. Find the greatest common factor of the two terms. The greatest common factor of 12 and 30 is 6.
2. Keep the greatest common factor outside the brackets, divide the polynomial terms by this factor and write the remaining expression inside the brackets. (12x + 30) = (6 ● 2x) + (6 ● 5) 6(2x + 5)
3. Verify your answer by multiplying the factors to get the original expression. 6(2x + 5) 12x + 30
Therefore, the area of each section of the garden is (2x + 5) square meters.
Practice Factoring Algebraic Expressions Word Problems
Practice Problem 1
Practice Problem 2
Practice Problem 3
Factor – is a number that divides the given number without any remainder.
Linear Expression – an algebraic expression in which the variable is raised to the first power, and variables are not multiplied or divided.
Term – either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or − signs.
Like terms – Terms that have the same power for the same variables. In like terms, one can only change the numerical coefficient.
Unlike terms – Terms that have different variables or the same variables raised to different powers.
Distributive Property – to multiply a sum or difference by a number, multiply each term inside the parenthesis by the number outside the parenthesis.
Constant – a term without a variable.
Variable – In algebra, a symbol (usually a letter) standing in for an unknown numerical value in an equation or expression.
Coefficient – is an integer that is multiplied with the variable of a single term or the terms of a polynomial.
Pre-requisite Skills Identify Factors Greatest Common Factor-GCF Arithmetic Sequences Geometric Sequences The Distributive Property Simplifying Complex Algebraic Expressions Add Linear Expressions Subtract Linear Expressions
Related Skills Solve One-Step Equations by Addition and Subtraction Solve One-Step Equations by Multiplying and Dividing Solve Equations with Rational Coefficients Solve Two-Step Equations Solve Complex Equations Solve Equations with Rational Coefficients Solve Two-Step Equations Write Two-Step Equations Solve Two-Sided Equations with Rational Coefficients Solve Multi-Step Equations

IMAGES
VIDEO
COMMENTS
Solving Problems by Factoring . Now that we know most of the factoring strategies for quadratic polynomials, we can apply these methods to solving real world problems. Real-World Application: Right Triangles . One leg of a right triangle is 3 feet longer than the other leg. The hypotenuse is 15 feet. Find the dimensions of the triangle.
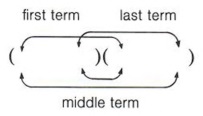
If you are factoring a quadratic like x^2+5x+4 you want to find two numbers that Add up to 5 Multiply together to get 4 Since 1 and 4 add up to 5 and multiply together to get 4, we can factor it like: (x+1)(x+4)
How do you solve factoring by greatest common monomial factor? ... (2×3=6), expressions have factors ((x+2)(x+3)=x^2+5x+6). Factoring is the process... Chat with Symbo. AI may present inaccurate or offensive content that does not represent Symbolab's views. Do not enter any personal information. Enter a problem.
Differences and Sums of Powers. Using the formula for the sum of a geometric sequence, it's easy to derive the general formula for difference of powers: . If , this creates the difference of squares factorization, . This leads to the difference of cubes factorization, In addition, if is odd: . This also leads to the formula for the sum of cubes,
Solving Polynomial Equations by Factoring The zero-product property is true for any number of factors that make up an equation. If an expression is equal to zero and can be factored into linear factors, then we will be able to set each factor equal to zero and solve for each equation.
Factoring. The process of factoring is essential to the simplification of many algebraic expressions and is a useful tool in solving higher degree equations. In fact, the process of factoring is so important that very little of algebra beyond this point can be accomplished without understanding it.
3 complete examples of solving quadratic equations using factoring by grouping are shown. Examples: Factor x(x + 1) - 5(x + 1) Solve 2x 2 + 5x + 2 = 0; Solve 7x 2 + 16x + 4 = 0; Solve 6x ... Try the given examples, or type in your own problem and check your answer with the step-by-step explanations. We welcome your feedback, comments and ...
Equation Calculator - Solve By Factoring Solves an entered equation by factoring, showing step-by-step work. Practice Problems / Worksheet Practice solving by factoring with 20 problems and solutions. Next Lesson: Quadratic Equations When you have a polynomial function of degree two, you have a quadratic function.
1. Read the word problem and determine the greatest common factor of the terms. 2. Keep the greatest common factor outside the brackets, divide the polynomial terms by this factor and write the remaining expression inside the brackets. 3. Verify your answer by multiplying the factors to get the original expression.
Factoring Method. Set the equation equal to zero, that is, get all the nonzero terms on one side of the equal sign and 0 on the other. \(ax^2 + bx + c = 0\) Factor the quadratic expression. \(()() = 0\) By the zero-factor property, at least one of the factors must be zero, so, set each of the factors equal to 0 and solve for the variable.