null hypothesis example between two variables

• Science, Tech, Math ›
• Chemistry ›
• Scientific Method ›

Null Hypothesis Examples

ThoughtCo / Hilary Allison

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating ​a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.

The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.

What Is the Null Hypothesis?

The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not​ need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.

To distinguish it from other hypotheses , the null hypothesis is written as ​ H 0  (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.

Examples of the Null Hypothesis

To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.

Other Types of Hypotheses

In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."

Key Takeaways

• In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
• Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
• By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
• What Are Examples of a Hypothesis?
• Random Error vs. Systematic Error
• Six Steps of the Scientific Method
• What Is a Hypothesis? (Science)
• Scientific Method Flow Chart
• What Are the Elements of a Good Hypothesis?
• Scientific Method Vocabulary Terms
• Understanding Simple vs Controlled Experiments
• The Role of a Controlled Variable in an Experiment
• What Is an Experimental Constant?
• What Is a Testable Hypothesis?
• Scientific Hypothesis Examples
• What Is the Difference Between a Control Variable and Control Group?
• DRY MIX Experiment Variables Acronym
• What Is a Controlled Experiment?
• Scientific Variable

15 Null Hypothesis Examples

Chris Drew (PhD)

Dr. Chris Drew is the founder of the Helpful Professor. He holds a PhD in education and has published over 20 articles in scholarly journals. He is the former editor of the Journal of Learning Development in Higher Education. [Image Descriptor: Photo of Chris]

Learn about our Editorial Process

A null hypothesis is a general assertion or default position that there is no relationship or effect between two measured phenomena.

It’s a critical part of statistics, data analysis, and the scientific method . This concept forms the basis of testing statistical significance and allows researchers to be objective in their conclusions.

A null hypothesis helps to eliminate biases and ensures that the observed results are not due to chance. The rejection or failure to reject the null hypothesis helps in guiding the course of research.

Null Hypothesis Definition

The null hypothesis, often denoted as H 0 , is the hypothesis in a statistical test which proposes no statistical significance exists in a set of observed data.

It hypothesizes that any kind of difference or importance you see in a data set is due to chance.

Null hypotheses are typically proposed to be negated or disproved by statistical tests, paving way for the acceptance of an alternate hypothesis.

Importantly, a null hypothesis cannot be proven true; it can only be supported or rejected with confidence.

Should evidence – via statistical analysis – contradict the null hypothesis, it is rejected in favor of an alternative hypothesis. In essence, the null hypothesis is a tool to challenge and disprove that there is no effect or relationship between variables.

Video Explanation

I like to show this video to my students which outlines a null hypothesis really clearly and engagingly, using real life studies by research students! The into explains it really well:

“There’s an idea in science called the null hypothesis and it works like this: when you’re setting out to prove a theory, your default answer should be “it’s not going to work” and you have to convince the world otherwise through clear results”

Here’s the full video:

Null Hypothesis Examples

• Equality of Means: The null hypothesis posits that the average of group A does not differ from the average of group B. It suggests that any observed difference between the two group means is due to sampling or experimental error.
• No Correlation: The null hypothesis states there is no correlation between the variable X and variable Y in the population. It means that any correlation seen in sample data occurred by chance.
• Drug Effectiveness: The null hypothesis proposes that a new drug does not reduce the number of days to recover from a disease compared to a standard drug. Any observed difference is merely by chance and not due to the new drug.
• Classroom Teaching Method: The null hypothesis states that a new teaching method does not result in improved test scores compared to the traditional teaching method. Any improvement in scores can be attributed to chance or other unrelated factors.
• Smoking and Life Expectancy: The null hypothesis asserts that the average life expectancy of smokers is the same as that of non-smokers. Any perceived difference in life expectancy is due to random variation or other factors.
• Brand Preference: The null hypothesis suggests that the proportion of consumers preferring Brand A is the same as those preferring Brand B. Any observed preference in the sample is due to random selection.
• Vaccination Efficacy: The null hypothesis states that the efficacy of Vaccine A does not differ from that of Vaccine B. Any differences observed in a sample are due to chance or other confounding factors.
• Diet and Weight Loss: The null hypothesis proposes that following a specific diet does not result in more weight loss than not following the diet. Any weight loss observed among dieters is considered random or influenced by other factors.
• Exercise and Heart Rate: The null hypothesis states that regular exercise does not lower resting heart rate compared to no exercise. Any lower heart rates observed in exercisers could be due to chance or other unrelated factors.
• Climate Change: The null hypothesis asserts that the average global temperature this decade is not higher than the previous decade. Any observed temperature increase can be attributed to random variation or unaccounted factors.
• Gender Wage Gap: The null hypothesis posits that men and women earn the same average wage for the same job. Any observed wage disparity is due to chance or non-gender related factors.
• Psychotherapy Effectiveness: The null hypothesis states that patients undergoing psychotherapy do not show more improvement than those not undergoing therapy. Any improvement in the
• Energy Drink Consumption and Sleep: The null hypothesis proposes that consuming energy drinks does not affect the quantity of sleep. Any observed differences in sleep duration among energy drink consumers is due to random variation or other factors.
• Organic Food and Health: The null hypothesis asserts that consuming organic food does not lead to better health outcomes compared to consuming non-organic food. Any health differences observed in consumers of organic food are considered random or attributed to other confounding factors.
• Online Learning Effectiveness: The null hypothesis states that students learning online do not perform differently on exams than students learning in traditional classrooms. Any difference in performance can be attributed to chance or unrelated factors.

Null Hypothesis vs Alternative Hypothesis

An alternative hypothesis is the direct contrast to the null hypothesis. It posits that there is a statistically significant relationship or effect between the variables being observed.

If the null hypothesis is rejected based on the test data, the alternative hypothesis is accepted.

Importantly, while the null hypothesis is typically a statement of ‘no effect’ or ‘no difference,’ the alternative hypothesis states that there is an effect or difference.

Comprehension Checkpoint: How does the null hypothesis help to ensure that research is objective and unbiased?

Applications of the Null Hypothesis in Research

The null hypothesis plays a critical role in numerous research settings, promoting objectivity and ensuring findings aren’t due to random chance.

• Clinical Trials: Null hypothesis is used extensively in medical and pharmaceutical research. For example, when testing a new drug’s effectiveness, the null hypothesis might state that the drug has no effect on the disease. If data contradicts this, the null hypothesis is rejected, suggesting the drug might be effective.
• Business and Economics: Businesses use null hypotheses to make informed decisions. For instance, a company might use a null hypothesis to test if a new marketing strategy improves sales. If data suggests a significant increase in sales, the null hypothesis is rejected, and the new strategy may be implemented.
• Psychological Research: Psychologists use null hypotheses to test theories about behavior. For instance, a null hypothesis might state there’s no link between stress and sleep quality. Rejecting this hypothesis based on collected data could help establish a correlation between the two variables.
• Environmental Science: Null hypotheses are used to understand environmental changes. For instance, researchers might form a null hypothesis stating there is no significant difference in air quality before and after a policy change. If this hypothesis is rejected, it indicates the policy may have impacted air quality.
• Education: Educators and researchers often use null hypotheses to improve teaching methods. For example, a null hypothesis might propose a new teaching technique doesn’t enhance student performance. If data contradicts this, the technique may be beneficial.

In all these areas, the null hypothesis helps minimize bias, enabling researchers to support their findings with statistically significant data. It forms the backbone of many scientific research methodologies , promoting a disciplined approach to uncovering new knowledge.

See More Hypothesis Examples Here

The null hypothesis is a cornerstone of statistical analysis and empirical research. It serves as a starting point for investigations, providing a baseline premise that the observed effects are due to chance. By understanding and applying the concept of the null hypothesis, researchers can test the validity of their assumptions, making their findings more robust and reliable. In essence, the null hypothesis ensures that the scientific exploration remains objective, systematic, and free from unintended bias.

• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ Free Social Skills Worksheets
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 10 Reasons you’re Perpetually Single
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 20 Montessori Toddler Bedrooms (Design Inspiration)
• Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 21 Montessori Homeschool Setups

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration

Null Hypothesis

Null Hypothesis , often denoted as H 0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effect occurring. The null is t he truth or falsity of an idea in analysis.

In this article, we will discuss the null hypothesis in detail, along with some solved examples and questions on the null hypothesis.

Table of Content

What is Null Hypothesis?

Null hypothesis symbol, formula of null hypothesis, types of null hypothesis, null hypothesis examples, principle of null hypothesis, how do you find null hypothesis, null hypothesis in statistics, null hypothesis and alternative hypothesis, null hypothesis and alternative hypothesis examples, null hypothesis - practice problems.

Null Hypothesis in statistical analysis suggests the absence of statistical significance within a specific set of observed data. Hypothesis testing, using sample data, evaluates the validity of this hypothesis. Commonly denoted as H 0 or simply "null," it plays an important role in quantitative analysis, examining theories related to markets, investment strategies, or economies to determine their validity.

Null Hypothesis Meaning

Null Hypothesis represents a default position, often suggesting no effect or difference, against which researchers compare their experimental results. The Null Hypothesis, often denoted as H 0 asserts a default assumption in statistical analysis. It posits no significant difference or effect, serving as a baseline for comparison in hypothesis testing.

The null Hypothesis is represented as H 0 , the Null Hypothesis symbolizes the absence of a measurable effect or difference in the variables under examination.

Certainly, a simple example would be asserting that the mean score of a group is equal to a specified value like stating that the average IQ of a population is 100.

The Null Hypothesis is typically formulated as a statement of equality or absence of a specific parameter in the population being studied. It provides a clear and testable prediction for comparison with the alternative hypothesis. The formulation of the Null Hypothesis typically follows a concise structure, stating the equality or absence of a specific parameter in the population.

Mean Comparison (Two-sample t-test)

H 0 : μ 1 = μ 2

This asserts that there is no significant difference between the means of two populations or groups.

Proportion Comparison

H 0 : p 1 − p 2 = 0

This suggests no significant difference in proportions between two populations or conditions.

Equality in Variance (F-test in ANOVA)

H 0 : σ 1 = σ 2

This states that there's no significant difference in variances between groups or populations.

Independence (Chi-square Test of Independence):

H 0 : Variables are independent

This asserts that there's no association or relationship between categorical variables.

Null Hypotheses vary including simple and composite forms, each tailored to the complexity of the research question. Understanding these types is pivotal for effective hypothesis testing.

Equality Null Hypothesis (Simple Null Hypothesis)

The Equality Null Hypothesis, also known as the Simple Null Hypothesis, is a fundamental concept in statistical hypothesis testing that assumes no difference, effect or relationship between groups, conditions or populations being compared.

Non-Inferiority Null Hypothesis

In some studies, the focus might be on demonstrating that a new treatment or method is not significantly worse than the standard or existing one.

Superiority Null Hypothesis

The concept of a superiority null hypothesis comes into play when a study aims to demonstrate that a new treatment, method, or intervention is significantly better than an existing or standard one.

Independence Null Hypothesis

In certain statistical tests, such as chi-square tests for independence, the null hypothesis assumes no association or independence between categorical variables.

Homogeneity Null Hypothesis

In tests like ANOVA (Analysis of Variance), the null hypothesis suggests that there's no difference in population means across different groups.

• Medicine: Null Hypothesis: "No significant difference exists in blood pressure levels between patients given the experimental drug versus those given a placebo."
• Education: Null Hypothesis: "There's no significant variation in test scores between students using a new teaching method and those using traditional teaching."
• Economics: Null Hypothesis: "There's no significant change in consumer spending pre- and post-implementation of a new taxation policy."
• Environmental Science: Null Hypothesis: "There's no substantial difference in pollution levels before and after a water treatment plant's establishment."

The principle of the null hypothesis is a fundamental concept in statistical hypothesis testing. It involves making an assumption about the population parameter or the absence of an effect or relationship between variables.

In essence, the null hypothesis (H 0 ) proposes that there is no significant difference, effect, or relationship between variables. It serves as a starting point or a default assumption that there is no real change, no effect or no difference between groups or conditions.

The null hypothesis is usually formulated to be tested against an alternative hypothesis (H 1 or H \alpha ) which suggests that there is an effect, difference or relationship present in the population.

Null Hypothesis Rejection

Rejecting the Null Hypothesis occurs when statistical evidence suggests a significant departure from the assumed baseline. It implies that there is enough evidence to support the alternative hypothesis, indicating a meaningful effect or difference. Null Hypothesis rejection occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

Identifying the Null Hypothesis involves defining the status quotient, asserting no effect and formulating a statement suitable for statistical analysis.

When is Null Hypothesis Rejected?

The Null Hypothesis is rejected when statistical tests indicate a significant departure from the expected outcome, leading to the consideration of alternative hypotheses. It occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

In statistical hypothesis testing, researchers begin by stating the null hypothesis, often based on theoretical considerations or previous research. The null hypothesis is then tested against an alternative hypothesis (Ha), which represents the researcher's claim or the hypothesis they seek to support.

The process of hypothesis testing involves collecting sample data and using statistical methods to assess the likelihood of observing the data if the null hypothesis were true. This assessment is typically done by calculating a test statistic, which measures the difference between the observed data and what would be expected under the null hypothesis.

In the realm of hypothesis testing, the null hypothesis (H 0 ) and alternative hypothesis (H₁ or Ha) play critical roles. The null hypothesis generally assumes no difference, effect, or relationship between variables, suggesting that any observed change or effect is due to random chance. Its counterpart, the alternative hypothesis, asserts the presence of a significant difference, effect, or relationship between variables, challenging the null hypothesis. These hypotheses are formulated based on the research question and guide statistical analyses.

Difference Between Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) serves as the baseline assumption in statistical testing, suggesting no significant effect, relationship, or difference within the data. It often proposes that any observed change or correlation is merely due to chance or random variation. Conversely, the alternative hypothesis (H 1 or Ha) contradicts the null hypothesis, positing the existence of a genuine effect, relationship or difference in the data. It represents the researcher's intended focus, seeking to provide evidence against the null hypothesis and support for a specific outcome or theory. These hypotheses form the crux of hypothesis testing, guiding the assessment of data to draw conclusions about the population being studied.

Let's envision a scenario where a researcher aims to examine the impact of a new medication on reducing blood pressure among patients. In this context:

Null Hypothesis (H 0 ): "The new medication does not produce a significant effect in reducing blood pressure levels among patients."

Alternative Hypothesis (H 1 or Ha): "The new medication yields a significant effect in reducing blood pressure levels among patients."

The null hypothesis implies that any observed alterations in blood pressure subsequent to the medication's administration are a result of random fluctuations rather than a consequence of the medication itself. Conversely, the alternative hypothesis contends that the medication does indeed generate a meaningful alteration in blood pressure levels, distinct from what might naturally occur or by random chance.

People Also Read:

Mathematics Maths Formulas Probability and Statistics

Example 1: A researcher claims that the average time students spend on homework is 2 hours per night.

Null Hypothesis (H 0 ): The average time students spend on homework is equal to 2 hours per night. Data: A random sample of 30 students has an average homework time of 1.8 hours with a standard deviation of 0.5 hours. Test Statistic and Decision: Using a t-test, if the calculated t-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: Based on the statistical analysis, we fail to reject the null hypothesis, suggesting that there is not enough evidence to dispute the claim of the average homework time being 2 hours per night.

Example 2: A company asserts that the error rate in its production process is less than 1%.

Null Hypothesis (H 0 ): The error rate in the production process is 1% or higher. Data: A sample of 500 products shows an error rate of 0.8%. Test Statistic and Decision: Using a z-test, if the calculated z-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: The statistical analysis supports rejecting the null hypothesis, indicating that there is enough evidence to dispute the company's claim of an error rate of 1% or higher.

Q1. A researcher claims that the average time spent by students on homework is less than 2 hours per day. Formulate the null hypothesis for this claim?

Q2. A manufacturing company states that their new machine produces widgets with a defect rate of less than 5%. Write the null hypothesis to test this claim?

Q3. An educational institute believes that their online course completion rate is at least 60%. Develop the null hypothesis to validate this assertion?

Q4. A restaurant claims that the waiting time for customers during peak hours is not more than 15 minutes. Formulate the null hypothesis for this claim?

Q5. A study suggests that the mean weight loss after following a specific diet plan for a month is more than 8 pounds. Construct the null hypothesis to evaluate this statement?

Summary - Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) and alternative hypothesis (H a ) are fundamental concepts in statistical hypothesis testing. The null hypothesis represents the default assumption, stating that there is no significant effect, difference, or relationship between variables. It serves as the baseline against which the alternative hypothesis is tested. In contrast, the alternative hypothesis represents the researcher's hypothesis or the claim to be tested, suggesting that there is a significant effect, difference, or relationship between variables. The relationship between the null and alternative hypotheses is such that they are complementary, and statistical tests are conducted to determine whether the evidence from the data is strong enough to reject the null hypothesis in favor of the alternative hypothesis. This decision is based on the strength of the evidence and the chosen level of significance. Ultimately, the choice between the null and alternative hypotheses depends on the specific research question and the direction of the effect being investigated.

FAQs on Null Hypothesis

What does null hypothesis stands for.

The null hypothesis, denoted as H 0 ​, is a fundamental concept in statistics used for hypothesis testing. It represents the statement that there is no effect or no difference, and it is the hypothesis that the researcher typically aims to provide evidence against.

How to Form a Null Hypothesis?

A null hypothesis is formed based on the assumption that there is no significant difference or effect between the groups being compared or no association between variables being tested. It often involves stating that there is no relationship, no change, or no effect in the population being studied.

When Do we reject the Null Hypothesis?

In statistical hypothesis testing, if the p-value (the probability of obtaining the observed results) is lower than the chosen significance level (commonly 0.05), we reject the null hypothesis. This suggests that the data provides enough evidence to refute the assumption made in the null hypothesis.

What is a Null Hypothesis in Research?

In research, the null hypothesis represents the default assumption or position that there is no significant difference or effect. Researchers often try to test this hypothesis by collecting data and performing statistical analyses to see if the observed results contradict the assumption.

What Are Alternative and Null Hypotheses?

The null hypothesis (H0) is the default assumption that there is no significant difference or effect. The alternative hypothesis (H1 or Ha) is the opposite, suggesting there is a significant difference, effect or relationship.

What Does it Mean to Reject the Null Hypothesis?

Rejecting the null hypothesis implies that there is enough evidence in the data to support the alternative hypothesis. In simpler terms, it suggests that there might be a significant difference, effect or relationship between the groups or variables being studied.

How to Find Null Hypothesis?

Formulating a null hypothesis often involves considering the research question and assuming that no difference or effect exists. It should be a statement that can be tested through data collection and statistical analysis, typically stating no relationship or no change between variables or groups.

How is Null Hypothesis denoted?

The null hypothesis is commonly symbolized as H 0 in statistical notation.

What is the Purpose of the Null hypothesis in Statistical Analysis?

The null hypothesis serves as a starting point for hypothesis testing, enabling researchers to assess if there's enough evidence to reject it in favor of an alternative hypothesis.

What happens if we Reject the Null hypothesis?

Rejecting the null hypothesis implies that there is sufficient evidence to support an alternative hypothesis, suggesting a significant effect or relationship between variables.

What are Test for Null Hypothesis?

Various statistical tests, such as t-tests or chi-square tests, are employed to evaluate the validity of the Null Hypothesis in different scenarios.

Similar Reads

• Null Hypothesis Null Hypothesis, often denoted as H0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effe 12 min read
• Hypothesis Testing Formula Statistics is a discipline of applied mathematics that deals with gathering, describing, analyzing, and inferring conclusions from numerical data. Differential and integral calculus, linear algebra, and probability theory are all used substantially in statistics' mathematical theories. Statisticians 8 min read
• SQL IS NULL The SQL IS NULL operator is a logical operator used to identify and filter out rows with NULL values in a column. A NULL value represents missing or undefined data in a database. It is different from a zero value or blank space, and it indicates that the value is unknown. In this article, we will le 4 min read
• SQLite IS NULL SQLite is a server-less database engine and it is written in c programming language. It is developed by D. Richard Hipp in the year 2000. The main moto for developing the SQLite is to escape from using the complex database engines like MYSQL.etc. It has become one of the most popular database engine 6 min read
• MySQL NOT NULL Constraint In the database management system maintaining data reliability and data accuracy is very important. MySQL is a popular relational database management system, which offers various constraints to provide security and ensure the integrity of the stored data. There are various key constraints present in 4 min read
• Permutation Hypothesis Test in R Programming In simple words, the permutation hypothesis test in R is a way of comparing a numerical value of 2 groups. The permutation Hypothesis test is an alternative to: Independent two-sample t-test Mann-Whitney U aka Wilcoxon Rank-Sum Test Let's implement this test in R programming. Why use the Permutation 6 min read
• Null in JavaScript In JavaScript, `null` indicates the deliberate absence of any object value. It's a primitive value that denotes the absence of a value or serves as a placeholder for an object that isn't present. `null` differs from `undefined`, which signifies a variable that has been declared but hasn't been assig 3 min read
• What is Null Session? The null session attack has been present since Windows 2000 was extensively used; yet, system administrators do not take this type of attack into account when implementing network security measures. This can have unimaginable consequences since hackers can use this type of attack to obtain all of th 4 min read
• How to Use the linearHypothesis() Function in R In statistics, understanding how variables relate to each other is crucial. This helps in making smart decisions. When we build regression models, we need to check if certain combinations of variables are statistically significant. In R Programming Language a tool called linear hypothesis () in the 4 min read
• What is /Dev/Null in Linux? If you have been learning shell programming, you may already have come across something like /dev/null. In this article, we will understand what it is and how it is used. Let's start off by understanding what /dev is. What is /dev?In the Linux file system, everything is a file or a directory. Even d 5 min read
• MySQL Handling NULL Values In MySQL, NULL values represent the absence of data or a missing value. Understanding how to handle NULL values is crucial for effective database management and querying. This article will cover various aspects of working with NULL how to handle them in queries, update statements, and table definiti 4 min read
• SQLite NOT NULL Constraint SQLite is a very lightweight and embedded Relational Database Management System (RDBMS). It requires very minimal configuration and it is self-contained. It is serverless, therefore it is a perfect fit for mobile applications, simple desktop applications, and embedded systems. While it may not be a 4 min read
• Why hypothesis testing is important in research ? Hypothesis Testing allows researchers to evaluate the validity of their assumptions and draw conclusions based on evidence. It provides a framework for making predictions and determining whether observed results are statistically significant or just occurred by chance. By applying various statistica 6 min read
• How to use Is Not Null in PySpark In data processing, handling null values is a crucial task to ensure the accuracy and reliability of the analysis. PySpark, the Python API for Apache Spark, provides powerful methods to handle null values efficiently. In this article, we will go through how to use the isNotNull method in PySpark to 4 min read
• MySQL IS NULL Operator The IS NULL operator in MySQL is a powerful tool for handling records with missing or incomplete data. It enables precise querying and data management by allowing users to identify and act upon fields where values are absent. In this article, We will learn about the MySQL IS NULL Operator by underst 3 min read
• Null Space of a Matrix Null space of a matrix is a fundamental concept in linear algebra that describes the set of all possible solutions to the equation Ax = 0, where A is a matrix and x is a vector. This space consists of vectors that, when multiplied by the matrix A, result in the zero vector. In simpler terms, if you 6 min read
• MariaDB Not Null Constraint MariaDB is an open-source relational database management system. In a relational database, data integrity is very important. So, we use the NOT NULL constraint to ensure the data integrity in a table within a database. So, In this article, we are going to discuss how a NOT NULL constraint helps to m 4 min read
• Testing Various Hypothesis Test for Coefficients in R Hypothesis testing plays a critical role in statistical modeling, helping us assess whether the independent variables (predictors) in a model significantly impact the dependent variable (outcome). In the context of regression analysis, testing the coefficients allows us to evaluate the significance 5 min read
• NULL Pointer in C++ A NULL Pointer in C++ indicates the absence of a valid memory address in C++. It tells that the pointer is not pointing to any valid memory location In other words, it has the value "NULL" (or 'nullptr' since C++11). This is generally done at the time of variable declaration to check whether the poi 4 min read
• Geeks Premier League
• School Learning
• Geeks Premier League 2023
• Math-Concepts

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

How to Write a Null Hypothesis (5 Examples)

A hypothesis test uses sample data to determine whether or not some claim about a population parameter is true.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter =,  ≤, ≥ some value

H A  (Alternative Hypothesis): Population parameter <, >, ≠ some value

Note that the null hypothesis always contains the equal sign .

We interpret the hypotheses as follows:

Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.

Alternative hypothesis: The sample data  does provide sufficient evidence to support the claim being made by an individual.

For example, suppose it’s assumed that the average height of a certain species of plant is 20 inches tall. However, one botanist claims the true average height is greater than 20 inches.

To test this claim, she may go out and collect a random sample of plants. She can then use this sample data to perform a hypothesis test using the following two hypotheses:

H 0 : μ ≤ 20 (the true mean height of plants is equal to or even less than 20 inches)

H A : μ > 20 (the true mean height of plants is greater than 20 inches)

If the sample data gathered by the botanist shows that the mean height of this species of plants is significantly greater than 20 inches, she can reject the null hypothesis and conclude that the mean height is greater than 20 inches.

Read through the following examples to gain a better understanding of how to write a null hypothesis in different situations.

Example 1: Weight of Turtles

A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles.

Here is how to write the null and alternative hypotheses for this scenario:

H 0 : μ = 300 (the true mean weight is equal to 300 pounds)

H A : μ ≠ 300 (the true mean weight is not equal to 300 pounds)

Example 2: Height of Males

It’s assumed that the mean height of males in a certain city is 68 inches. However, an independent researcher believes the true mean height is greater than 68 inches. To test this, he goes out and collects the height of 50 males in the city.

H 0 : μ ≤ 68 (the true mean height is equal to or even less than 68 inches)

H A : μ > 68 (the true mean height is greater than 68 inches)

Example 3: Graduation Rates

A university states that 80% of all students graduate on time. However, an independent researcher believes that less than 80% of all students graduate on time. To test this, she collects data on the proportion of students who graduated on time last year at the university.

H 0 : p ≥ 0.80 (the true proportion of students who graduate on time is 80% or higher)

H A : μ < 0.80 (the true proportion of students who graduate on time is less than 80%)

Example 4: Burger Weights

A food researcher wants to test whether or not the true mean weight of a burger at a certain restaurant is 7 ounces. To test this, he goes out and measures the weight of a random sample of 20 burgers from this restaurant.

H 0 : μ = 7 (the true mean weight is equal to 7 ounces)

H A : μ ≠ 7 (the true mean weight is not equal to 7 ounces)

Example 5: Citizen Support

A politician claims that less than 30% of citizens in a certain town support a certain law. To test this, he goes out and surveys 200 citizens on whether or not they support the law.

H 0 : p ≥ .30 (the true proportion of citizens who support the law is greater than or equal to 30%)

H A : μ < 0.30 (the true proportion of citizens who support the law is less than 30%)

Additional Resources

Introduction to Hypothesis Testing Introduction to Confidence Intervals An Explanation of P-Values and Statistical Significance

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “How to Write a Null Hypothesis (5 Examples)”

you are amazing, thank you so much

Say I am a botanist hypothesizing the average height of daisies is 20 inches, or not? Does T = (ave – 20 inches) / √ variance / (80 / 4)? … This assumes 40 real measures + 40 fake = 80 n, but that seems questionable. Please advise.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating ​ the dependent variable or due to random chance. 

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

When do we reject the null hypothesis .

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected. 

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables. 

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a  p  -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

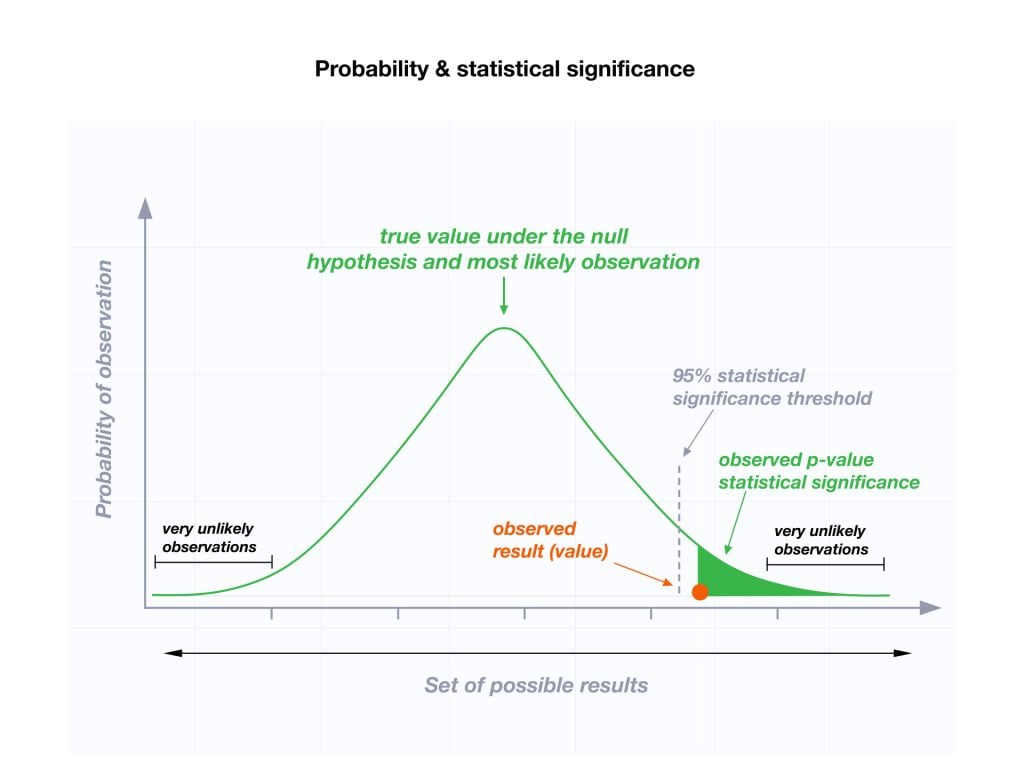
Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. 

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null. 

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists. 

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter. 

Purpose of a Null Hypothesis 

• The primary purpose of the null hypothesis is to disprove an assumption. 
• Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
• A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true. 

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables. 

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study. 

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”).  However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing.  Political research quarterly ,  52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method.  American Psychologist ,  56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing.  Behavior research methods ,  43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy.  Psychological methods ,  5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test.  Psychological bulletin ,  57 (5), 416.

• Science Notes Posts
• Contact Science Notes
• Todd Helmenstine Biography
• Anne Helmenstine Biography
• Free Printable Periodic Tables (PDF and PNG)
• Periodic Table Wallpapers
• Interactive Periodic Table
• Periodic Table Posters
• Science Experiments for Kids
• How to Grow Crystals
• Chemistry Projects
• Fire and Flames Projects
• Holiday Science
• Chemistry Problems With Answers
• Physics Problems
• Unit Conversion Example Problems
• Chemistry Worksheets
• Biology Worksheets
• Periodic Table Worksheets
• Physical Science Worksheets
• Science Lab Worksheets
• My Amazon Books

Null Hypothesis Examples

The null hypothesis (H 0 ) is the hypothesis that states there is no statistical difference between two sample sets. In other words, it assumes the independent variable does not have an effect on the dependent variable in a scientific experiment .

The null hypothesis is the most powerful type of hypothesis in the scientific method because it’s the easiest one to test with a high confidence level using statistics. If the null hypothesis is accepted, then it’s evidence any observed differences between two experiment groups are due to random chance. If the null hypothesis is rejected, then it’s strong evidence there is a true difference between test sets or that the independent variable affects the dependent variable.

• The null hypothesis is a nullifiable hypothesis. A researcher seeks to reject it because this result strongly indicates observed differences are real and not just due to chance.
• The null hypothesis may be accepted or rejected, but not proven. There is always a level of confidence in the outcome.

What Is the Null Hypothesis?

The null hypothesis is written as H 0 , which is read as H-zero, H-nought, or H-null. It is associated with another hypothesis, called the alternate or alternative hypothesis H A or H 1 . When the null hypothesis and alternate hypothesis are written mathematically, they cover all possible outcomes of an experiment.

An experimenter tests the null hypothesis with a statistical analysis called a significance test. The significance test determines the likelihood that the results of the test are not due to chance. Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01). But, even if the confidence in the test is high, there is always a small chance the outcome is incorrect. This means you can’t prove a null hypothesis. It’s also a good reason why it’s important to repeat experiments.

Exact and Inexact Null Hypothesis

The most common type of null hypothesis assumes no difference between two samples or groups or no measurable effect of a treatment. This is the exact hypothesis . If you’re asked to state a null hypothesis for a science class, this is the one to write. It is the easiest type of hypothesis to test and is the only one accepted for certain types of analysis. Examples include:

There is no difference between two groups H 0 : μ 1  = μ 2 (where H 0  = the null hypothesis, μ 1  = the mean of population 1, and μ 2  = the mean of population 2)

Both groups have value of 100 (or any number or quality) H 0 : μ = 100

However, sometimes a researcher may test an inexact hypothesis . This type of hypothesis specifies ranges or intervals. Examples include:

Recovery time from a treatment is the same or worse than a placebo: H 0 : μ ≥ placebo time

There is a 5% or less difference between two groups: H 0 : 95 ≤ μ ≤ 105

An inexact hypothesis offers “directionality” about a phenomenon. For example, an exact hypothesis can indicate whether or not a treatment has an effect, while an inexact hypothesis can tell whether an effect is positive of negative. However, an inexact hypothesis may be harder to test and some scientists and statisticians disagree about whether it’s a true null hypothesis .

How to State the Null Hypothesis

To state the null hypothesis, first state what you expect the experiment to show. Then, rephrase the statement in a form that assumes there is no relationship between the variables or that a treatment has no effect.

Example: A researcher tests whether a new drug speeds recovery time from a certain disease. The average recovery time without treatment is 3 weeks.

• State the goal of the experiment: “I hope the average recovery time with the new drug will be less than 3 weeks.”
• Rephrase the hypothesis to assume the treatment has no effect: “If the drug doesn’t shorten recovery time, then the average time will be 3 weeks or longer.” Mathematically: H 0 : μ ≥ 3

This null hypothesis (inexact hypothesis) covers both the scenario in which the drug has no effect and the one in which the drugs makes the recovery time longer. The alternate hypothesis is that average recovery time will be less than three weeks:

H A : μ < 3

Of course, the researcher could test the no-effect hypothesis (exact null hypothesis): H 0 : μ = 3

The danger of testing this hypothesis is that rejecting it only implies the drug affected recovery time (not whether it made it better or worse). This is because the alternate hypothesis is:

H A : μ ≠ 3 (which includes μ <3 and μ >3)

Even though the no-effect null hypothesis yields less information, it’s used because it’s easier to test using statistics. Basically, testing whether something is unchanged/changed is easier than trying to quantify the nature of the change.

Remember, a researcher hopes to reject the null hypothesis because this supports the alternate hypothesis. Also, be sure the null and alternate hypothesis cover all outcomes. Finally, remember a simple true/false, equal/unequal, yes/no exact hypothesis is easier to test than a more complex inexact hypothesis.

• Adèr, H. J.; Mellenbergh, G. J. & Hand, D. J. (2007).  Advising on Research Methods: A Consultant’s Companion . Huizen, The Netherlands: Johannes van Kessel Publishing. ISBN  978-90-79418-01-5 .
• Cox, D. R. (2006).  Principles of Statistical Inference . Cambridge University Press. ISBN  978-0-521-68567-2 .
• Everitt, Brian (1998).  The Cambridge Dictionary of Statistics . Cambridge, UK New York: Cambridge University Press. ISBN 978-0521593465.
• Weiss, Neil A. (1999).  Introductory Statistics  (5th ed.). ISBN 9780201598773.

Related Posts

• Math Article

Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .

In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.

Table of contents:

• Comparison with Alternative Hypothesis

Null Hypothesis Definition

The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .

Null Hypothesis Symbol

In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .

Null Hypothesis Principle

The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.

Null Hypothesis Formula

Here, the hypothesis test formulas are given below for reference.

The formula for the null hypothesis is:

H 0 :  p = p 0

The formula for the alternative hypothesis is:

H a = p >p 0 , < p 0 ≠ p 0

The formula for the test static is:

Remember that,  p 0  is the null hypothesis and p – hat is the sample proportion.

Also, read:

Types of Null Hypothesis

There are different types of hypothesis. They are:

Simple Hypothesis

It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.

Composite Hypothesis

The composite hypothesis is one that does not completely specify the population distribution.

Exact Hypothesis

Exact hypothesis defines the exact value of the parameter. For example μ= 50

Inexact Hypothesis

This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60

Null Hypothesis Rejection

Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.

How do you Find the Null Hypothesis?

The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).

When is Null Hypothesis Rejected?

The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.

Null Hypothesis and Alternative Hypothesis

Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.

Null Hypothesis Examples

Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.

If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.

Few more examples are:

1). Are there is 100% chance of getting affected by dengue?

Ans: There could be chances of getting affected by dengue but not 100%.

2). Do teenagers are using mobile phones more than grown-ups to access the internet?

Ans: Age has no limit on using mobile phones to access the internet.

3). Does having apple daily will not cause fever?

Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.

4). Do the children more good in doing mathematical calculations than grown-ups?

Ans: Age has no effect on Mathematical skills.

In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives. 

The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data. 

Frequently Asked Questions on Null Hypothesis

What is meant by the null hypothesis.

In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.

What are the benefits of hypothesis testing?

Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.

When a null hypothesis is accepted and rejected?

The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.

Why is the null hypothesis important?

The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.

How to accept or reject the null hypothesis in the chi-square test?

If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

10.1 - setting the hypotheses: examples.

A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.

Example 10.2: Hypotheses with One Sample of One Categorical Variable Section  

About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.

• Research Question : Are artists more likely to be left-handed than people found in the general population?
• Response Variable : Classification of the student as either right-handed or left-handed

State Null and Alternative Hypotheses

• Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
• Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.

Example 10.3: Hypotheses with One Sample of One Measurement Variable Section  

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.

• Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
• Response Variable : dosage of the active ingredient found by a chemical assay.
• Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
• Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.

Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section  

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.

• Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
• Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
• Explanatory (Grouping) Variable: Sex
• Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
• Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.

Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section  

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.

• Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
• Response Variable : Weight loss (pounds)
• Explanatory (Grouping) Variable : Type of diet
• Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
• Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.

Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section  

• Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
• Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
• Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
• Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.

This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.

Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section  

• Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
• Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
• Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
• Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.

Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section  

• Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
• Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
• Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
• Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.