kein laplace experiment

Teste dein Wissen zum Thema Laplace Experiment!

Laplace experiment.

In diesem Artikel dreht sich alles um Laplace . Von der Laplace Wahrscheinlichkeit bis hin zum Laplace Würfel wird dir alles zu Laplace Experimenten erklärt.

Du möchtest wissen:  Was ist ein Laplace Experiment ? In unsrem Video erfährst du bequem und einfach was genau es bedeutet, wenn einem Zufallsexperiment die Laplace Bedingung zugrunde liegt.

Laplace Experiment Definition

Laplace wahrscheinlichkeit, laplace experiment aufgaben, laplace experiment — häufigste fragen, wahrscheinlichkeitsrechnung.

Ein Laplace Experiment ist ein Zufallsexperiment, bei dem alle elementaren Ergebnisse die selbe Wahrscheinlichkeit haben. Die dazugehörige Laplace Wahrscheinlichkeit wird mit der Laplace Formel berechnet, welche sich durch die Division der Anzahl des Ereignisses durch alle möglichen Ergebnisse ergibt.

Laplace Experiment Erklärung

Generell unterscheidet man in der Statistik unterscheidet verschiedene Spezialfälle von Wahrscheinlichkeiten. Einer dieser Sonderfälle ist die Laplace Wahrscheinlichkeit . Diese liegt den dazugehörigen Laplace Experimenten zugrunde und setzt voraus, dass alle elementaren Ergebnisse des Zufallsexperimentes die gleiche Wahrscheinlichkeit haben. Einfach gesagt, muss jedes mögliches Szenario gleich wahrscheinlich sein, damit von Laplace die Rede sein kann.

Laplace Experiment Beispiele

Das gängigste Beispiel für einen Laplace Versuch ist das Werfen eines ungezinkten Würfels. Ungezinkt bedeutet, dass dieser nicht manipuliert ist und, dass alle sechs Seiten mit gleicher Wahrscheinlichkeit gewürfelt werden. Bei einem Laplace Würfel fällt die 1 also genau gleich oft wie die 6, wenn man unendlich oft würfeln würde. Weitere Beispiele sind das Werfen einer Münze oder das drehen an einem Glücksrad. Die Wahrscheinlichkeit Kopf oder Zahl zu werfen beträgt dann nämlich jeweils genau 50%. Bei dem letzteren Beispiel muss zusätzlich beachten werden, dass alle möglichen Felder gleich häufig vorkommen müssen, damit die Laplace Bedingung erfüllt ist.

Du weist jetzt, dass jedem Laplace Experiment die Laplace Wahrscheinlichkeit zugrunde liegt. Die Bedingung, dass alle Versuchsausgänge gleich wahrscheinlich sind muss also erfüllt sein. Aber woher weiß man, ob diese Grundbedingung gegeben ist oder nicht?

Kein Laplace Experiment?

Wenn du also die Wahrscheinlichkeit für ein Ereignis bestimmen sollst, prüfe zunächst ob es sich bei dem Zufallsexperiment überhaupt um einen Laplace Versuch handelt oder nicht. Hier spricht man auch vom sogenannten Elementarereignis ω , also einem Ereignis, für das die Eintrittswahrscheinlichkeit immer gleich hoch ist. Es gilt:

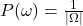
Laplace Formel

Allgemein ist die Wahrscheinlichkeit in einem Laplace Experiment für ein Ereignis A durch die Laplace Formel wie folgt definiert:

Abschließend schauen wir uns noch zwei praktische Beispiele von Laplace Experimenten an. So wird deutlich wie man die Wahrscheinlichkeit dieser Zufallsexperimente einfach mit der Laplace Formel berechnen kann.

Laplace Würfel

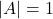
Laplace Experiment Beispiel: Roulette

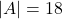
Die Wahrscheinlichkeit eine rote Zahl zu würfeln liegt also bei ungefähr 49%.

Das war auch schon alles Wichtige ! Zur Wiederholung hier nochmal die zentrale Formel:

• Was ist ein Laplace Experiment? Ein Laplace Experiment ist ein Zufallsexperiment, bei dem alle Ergebnisse dieselbe Wahrscheinlichkeit haben, einzutreffen. Ein typisches Beispiel hierfür ist der Wurf eines Würfels. Jede Augenzahl hat dieselbe Wahrscheinlichkeit gewürfelt zu werden, nämlich 1/6.   
• Was ist die Laplace Formel? Die Laplace Formel bestimmt die Wahrscheinlichkeit eines Ereignisses (E) im Laplace Experiment. Wenn die Gesamtzahl aller möglichen Ergebnisse n ist, berechnet sich die Wahrscheinlichkeit mit P(E) = 1/n.  
• Wie läuft ein Laplace Versuch ab? In einem Laplace Versuch (Experiment) müssen alle möglichen Ereignisse mit gleicher Wahrscheinlichkeit stattfinden. Das heißt, dass jedes zufällige Ergebnis gleich hohe Chancen hat, einzutreffen. Ein typisches Beispiel für ein Laplace Versuch ist der Wurf eines fairen Würfels.

Neben dem Laplace Experiment gibt es noch andere Zufallsexperimente. Wie du dann die Wahrscheinlichkeit berechnest , erfährst du hier!

Beliebte Inhalte aus dem Bereich Wahrscheinlichkeitsrechnung

• Bedingte Wahrscheinlichkeit Dauer: 02:16
• Vierfeldertafel Dauer: 04:46
• Satz der totalen Wahrscheinlichkeit Dauer: 01:58

Weitere Inhalte: Wahrscheinlichkeitsrechnung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke! Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung . Bitte lade anschließend die Seite neu .

Mathe matik

kapiert.de kann mehr!

• Übung starten
• Trainer starten
• Lern­manager öffnen
• Wahrscheinlichkeiten bestimmen bei Nicht-Laplace-Experimenten

Reißzweckenwurf

Es gibt Zufallsexperimente , deren Ausgänge nicht gleich wahrscheinlich sind. Nimm eine Reißzwecke und wirf sie auf den Boden. Wie du auf der Abbildung siehst, kann sie in zwei Positionen liegen bleiben. Diese Positionen heißen meistens Kopf und Seite .

Tom führt den Reißzweckenwurf sehr oft durch und trägt seine Ergebnisse in eine Tabelle ein.

Tom nimmt an, dass die relative Häufigkeit für das Zufallsexperiment eine gute Prognose für die Wahrscheinlichkeit der Ergebnisse „Kopf“ und „Seite“ ist. Aus der Tabelle folgt, dass die Ergebnisse nicht gleich wahrscheinlich sind. Solche Zufallsexperimente heißen Nicht-Laplace-Experimente .

Laplace-Experimente

Zufallsexperimente , bei denen alle Ergebnisse gleich wahrscheinlich sind, werden Laplace-Experimente genannt.

Reißzweckenwurf - Fortsetzung

Die im Zufallsexperiment ermittelten Wahrscheinlichkeiten p(E:„Kopf“) = 0,4 =40 % und p(F:„Seite“) = 0,6 = 60 % gelten nicht für alle Reißzwecken. Oft unterscheiden sich diese hinsichtlich ihrer Bauart. Daher kann die Wahrscheinlichkeit für eine bestimmte Reißzwecke nur über sehr viele Würfe abgeschätzt werden.

Für Nicht-Laplace-Experimente gilt folgende Aussage:

Die Wahrscheinlichkeit eines Ereignisses entspricht ungefähr der relativen Häufigkeit dieses Ereignisses bei einer großen Zahl von Versuchen.

Trotz dieser Unbestimmtheit gelten auch für Nicht-Laplace-Experimente bestimmte Gesetze.

Die Summe der Wahrscheinlichkeiten aller möglichen Ergebnisse eines Zufallsexperiments ist 1 (Summensatz). Sind die Ereignisse $$E$$ und $$bar E$$ eines Zufallsexperiments Gegenereignisse, so gilt p($$bar E$$) = 1 - p($$E$$) und p($$E$$) = 1 - p($$bar E$$).

Beipiel : Reißzweckenwurf Es gilt p(E:„Kopf“) + p(F:„Seite“) = 0,4 + 0,6 = 1. p(F:„Seite“) ist das Gegenereignis zu p(E:„Kopf“), daher gilt z.B. p(E:„Kopf“) = 1 - p(F:„Seite“) = 1 - 0,6 = 0,4

Der Lego-Achter

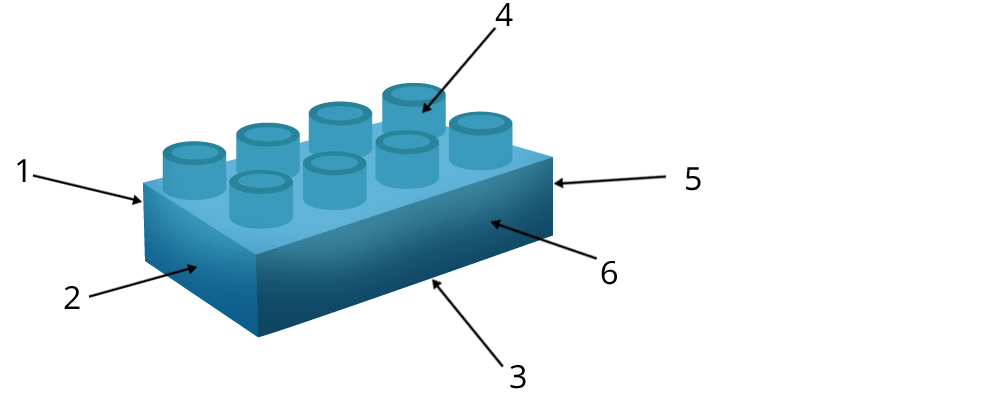
Du kennst sicher Legosteine. Mit solchen Steinen kannst du auch Zufallsexperimente durchführen. In der Tabelle sind die Ergebnisse zahlreicher Wurfexperimente für den Lego-Achter dargestellt.

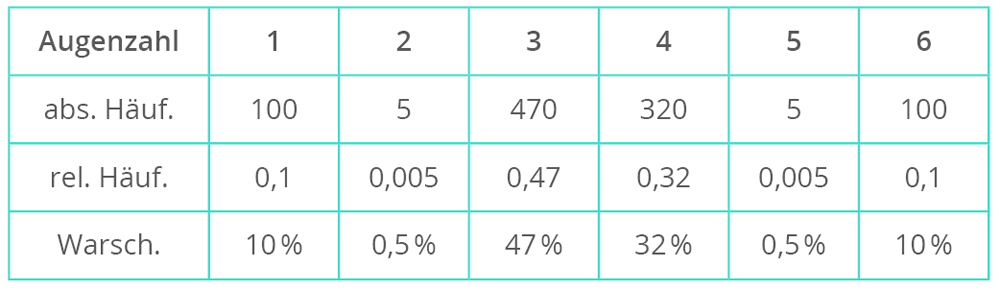
Das Wurfexperiment mit dem Lego-Achter ist ein Nicht-Laplace-Experiment . Du erkennst das daran, dass die Ergebnisse nicht gleich wahrscheinlich sind. Du kannst aber mit den Wahrscheinlichkeiten arbeiten: p(E:„ungerade Zahl“) = 0,1 + 0,47 + 0,005 = 0,575 = 57,5 % p(F:„gerade Zahl“) = 0,005 + 0,32 + 0,1 = 0,425 = 42,5 % p(E) + p(F) = 0,575 + 0,425 = 1 = 100 % p(G:„5 oder 6“) = 0,005 + 0,1 = 0,105 = 10,5 %.

Noch nicht kapiert?

kapiert.de kann mehr:

• interaktive Übungen und Tests
• individueller Klassenarbeitstrainer
• Lernmanager

Umfragen in der Bevölkerung können als Zufallsexperimente aufgefasst werden. Dabei handelt es sich auch um Nicht-Laplace-Experimente .

Bei einer Befragung zum Bau eines neuen Flughafens in A-Stadt haben sich die befragten Personen so entschieden, wie es in der Abbildung dargestellt ist (A: Zustimmung, B: Ablehnung, C: keine Meinung, D : sonstiges).

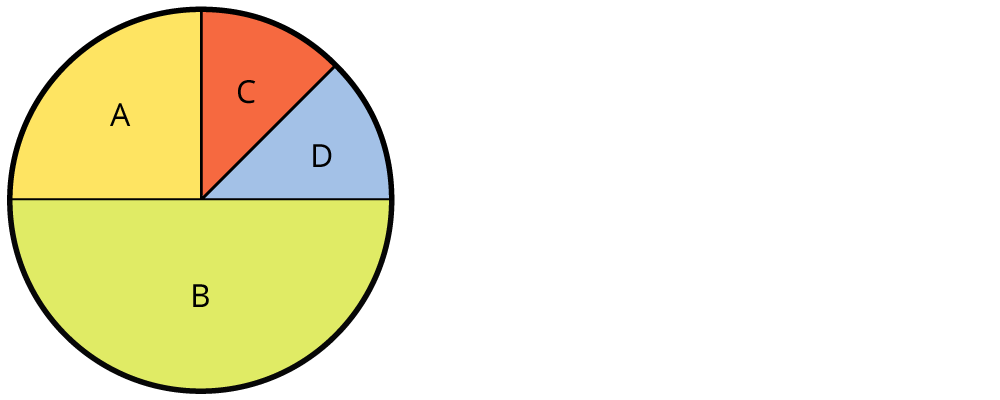
1. Wie groß ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte befragte Person „Zustimmung“ äußerte? Antwort : Die Wahrscheinlichkeit beträgt 25 %. 2. Wie groß ist die Wahrscheinlichkeit, dass eine zufällig befragte Person „weder Zustimmung noch Ablehnung“ äußerte? Antwort : Es wird mit Hilfe der Gegenwahrscheinlichkeit berechnet: p(„weder A noch B“) = 1 - [p(A) + p(B)] = 1 - [25% + 50%] = 1 - 75 % = 25 %.

• Wahrscheinlichkeiten bestimmen bei einstufigen Zufallsexperimenten
• Baumdiagramme zeichnen und Multiplikationsregel
• Baumdiagramme und Additionsregel
• Ereignis und Gegenereignis

kapiert.de passt zu deinem Schulbuch!    Buchreihen Mathematik     mein Schulbuch suchen

• Verstehen Üben Testen
• Klassenarbeitstrainer

Jetzt kostenlos testen

Das Thema macht dir noch Schwierigkeiten? Teste drei Tage das Lernportal von kapiert.de !

• Interaktive Übungen helfen dir beim Lernen.
• Videos, Audios und Grafiken erklären dir jedes Thema.
• Mit dem Klassenarbeitstrainer bereitest du dich auf deine Mathe-Klausur vor.
• Mit dem Lernmanager hast du alle Aufgaben im Blick.

Genau das Richtige lernen – mit kapiert.de drei Tage kostenlos. Die Testlizenz endet automatisch!

Das Kennwort muss mindestens 5 Zeichen lang sein.

Die angegebenen Passwörter stimmen nicht überein!

* Pflichtfelder

Das Thema Wahrscheinlichkeiten berechnen macht dir noch Schwierigkeiten?

kapiert.de hilft dir beim Lernen:

• Interaktive Übungen
• Klassen­arbeits­trainer
• Lern­manager

Teste das Lernportal von kapiert.de jetzt drei Tage kostenlos! Die Testlizenz endet automatisch!

3   Wahrscheinlichkeit

3.1 definition.

Manche Ereignisse sind weniger wahrscheinlich als andere. Wie hoch die Wahrscheinlichkeit eines Ereignisses ist, wird durch eine Abbildung (Funktion) angegeben.

Eine Abbildung \(P: A \mapsto P(A)\) heißt Wahrscheinlichkeit (engl. probability), wenn gilt

Nichtnegativität: \(P(A)\ge 0\) für alle Ereignisse \(A\)

Normierung: \(P(\Omega)=1\)

Additivität: Für disjunkte Ereignisse \(A\) und \(B\) (d.h. \(A\cap B=\emptyset\) ) ist \[ P(A\cup B)=P(A)+P(B). \]

Diese Eigenschaften, die eine Wahrscheinlichkeit erfüllen muss, sind intuitiv sinnvoll und können nicht aus irgendwelchen Fakten hergeleitet werden, daher spricht man auch von Axiomen . Etwas allgemeiner und präziser wurden diese Axiome 1933 von Andrey Kolmogorov (1903-1987) für eine saubere mathematische Fundierung der Wahrscheinlichkeitstheorie eingeführt.

Aus diesen Axiomen lassen sich einige Rechenregeln ableiten, zum Beispiel:

Komplementärereignis: \(P(\bar A)=1-P(A)\)

Additionssatz: \(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)

Monotonität: Wenn \(A\subseteq B\) , dann ist \(P(A)\le P(B)\) .

3.2 Laplace-Experimente

Eine besonders einfache Art von Zufallsvorgängen sind die sogenannten Laplace-Experimente.

Ein Zufallsvorgang heißt Laplace-Experiment (engl. Laplace experiment), wenn es nur endlich viele Ergebnisse gibt (d.h. wenn \(|\Omega|=n\) ) und wenn alle Elementarereignisse als gleich wahrscheinlich angenommen werden können.

Bei einem Laplace-Experiment ist die Wahrscheinlichkeit, dass ein Ergebnis \(A\) eintritt, leicht zu ermitteln. Sie beträgt \[ P(A)=\frac{|A|}{|\Omega|}, \] also die Anzahl der Ergebnisse in \(A\) dividiert durch die Anzahl aller Ergebnisse. Um Aussagen über Wahrscheinlichkeiten zu treffen, muss man also abzählen, wie viele Ergebnisse in den Mengen sind. Das ist manchmal sehr einfach, kann aber bei großen Mengen kompliziert sein. In solchen Fällen hilft der Teilbereich der Mathematik weiter, den man “Kombinatorik” nennt. Wir gehen in diesem Kurs jedoch nicht näher auf kombinatorische Probleme ein, sondern beschränken uns auf Mengen, bei denen es einfach ist, die Anzahl ihrer Elemente zu bestimmen.

Ein Würfel wird geworfen. Es handelt sich um ein Laplace-Experiment. Die Anzahl der Ergebnisse in \(\Omega\) beträgt 6. Sei \(A\) das Ereignis “Eine gerade Zahl wird geworfen”, also \(A=\{2,4,6\}\) . Dann ist

\[\begin{align*} P(A)&=\frac{|A|}{|\Omega|}\\ &=\frac{3}{6}\\ &=0.5. \end{align*}\]

Zwei gleich aussehende Würfel werden geworfen. Nun spielt es eine Rolle, wie man die Ergebnismenge festlegt. Wir wählen

\[\begin{align*} \Omega=\{&11,12,13,14,15,16,\\ &21,22,23,24,25,26,\\ &31,32,33,34,35,36,\\ &41,42,43,44,45,46,\\ &51,52,53,54,55,56,\\ &61,62,63,64,65,66\} \end{align*}\]

weil es sich dann um ein Laplace-Experiment handelt. Die Ergebnisse “24” und “42” sind zwar nicht unterscheidbar, wenn die Würfel gleich aussehen, aber wir können den zuerst geworfenen Würfel (oder z.B. den weiter links liegenden) als ersten Würfel bezeichnen. Dass alle 36 Ergebnisse gleich wahrscheinlich sind, können wir (nur) mit unserem Alltagswissen begründen, nicht aus der Mathematik heraus.

Sei \(A\) das Ereignis “Die Augenzahlen der beiden Würfel unterscheiden sich um 2”, d.h. \[ A=\{13,24,31,35,42,46,53,64\}. \] Dann gilt \[\begin{align*} P(A)&=\frac{|A|}{|\Omega|}\\ &=\frac{8}{36}\\ &=\frac{2}{9}\\ &\approx 0.2222. \end{align*}\]

Da die beiden Würfel nicht unterscheidbar sind, wäre als Ergebnismenge auch

\[\begin{align*} \Omega=\{ &11,12,13,14,15,16,\\ &22,23,24,25,26,\\ &33,34,35,36,\\ &44,45,46,\\ &55,56,\\ &66\} \end{align*}\]

möglich gewesen. Die Ergebnismenge hätte dann 21 Elemente. Die Annahme eines Laplace-Experiments wäre jedoch in diesem Fall nicht mehr korrekt, denn die Elementarereignisse “11” und “12” sind beispielsweise nicht gleich wahrscheinlich. Wir wissen aus unserer Erfahrung, dass ein Pasch seltener auftritt.

Die Wahl der Ergebnismenge sollte immer so erfolgen, dass das weitere Vorgehen möglichst einfach und elegant ist. Wenn die Ergebnismenge so gewählt werden kann, dass ein Laplace-Experiment vorliegt, sollte man das tun.

3.3 Bedingte Wahrscheinlichkeit

Manchmal gibt es begrenzte Informationen über einen Zufallsvorgang. Dann kennt man zwar nicht das realisierte Ergebnis, kann aber die Menge der möglichen Ergebnisse eingrenzen. Dadurch ändern sich die Wahrscheinlichkeiten für Ereignisse.

Wir betrachten zwei Ereignsse \(A\) und \(B\) mit \(P(B)>0\) . Dann heißt \[ P(A|B)=\frac{P(A\cap B)}{P(B)} \] die bedingte Wahrscheinlichkeit (engl. conditional probability) von \(A\) gegeben \(B\) .

Die Notation \(A|B\) steht nicht für ein bestimmtes Ereignis, sondern zeigt an, dass wir eine neue Art von Wahrscheinlichkeit betrachten, nämlich die bedingte Wahrscheinlichkeit. Beim Sprechen über Wahrscheinlichkeiten ist es nicht immer einfach (aber sehr wichtig!), zwischen der Wahrscheinlichkeit \(P(A\cap B)\) und der bedingten Wahrscheinlichkeit \(P(A|B)\) zu unterscheiden. Wenn man \(P(A\cap B)\) meint, spricht man von der Wahrscheinlichkeit, dass \(A\) und \(B\) eintreten. Wenn man \(P(A|B)\) meint, sagt man \(A\) gegeben \(B\) , oder: \(A\) wenn \(B\) , oder: \(A\) unter der Bedingung \(B\) . Wenn man ausdrücklich angeben möchte, dass eine Wahrscheinlichkeit keine bedingte Wahrscheinlichkeit ist, nennt man sie auch eine unbedingte Wahrscheinlichkeit (engl. unconditional probability).

Ein Würfel wird geworfen. Wir betrachten die beiden Ereignisse \(A=\{2,4,6\}\) (“gerade Zahl”), und \(B=\{3,4,5,6\}\) (“eine Zahl größer als 2”). Die bedingte Wahrscheinlichkeit von \(A\) gegeben \(B\) beträgt

\[\begin{align*} P(A|B)&=\frac{P(A\cap B)}{P(B)}\\ &=\frac{P(\{4,6\})}{P(\{3,4,5,6\})}\\ &=\frac{1}{2} \end{align*}\]

und die bedingte Wahrscheinlichkeit von \(B\) gegeben \(A\) lautet

\[\begin{align*} P(B|A)&=\frac{P(B\cap A)}{P(A)}\\ &=\frac{P(\{4,6\})}{P(\{2,4,6\})}\\ &=\frac{2}{3}. \end{align*}\]

Zwei Würfel werden geworfen, ohne dass Sie es sehen können. Sie fragen, ob eine Sechs geworfen wurde. Die Frage wird wahrheitsgemäß bejaht. Wie groß ist die Wahrscheinlichkeit, dass ein 6er-Pasch geworfen wurde?

Sei \(A\) das Ereignis “6er-Pasch” und \(B\) das Ereignis “mindest eine Sechs wurde geworfen”, d.h.

\[\begin{align*} A &= \{66\}\\ B &= \{16,26,36,46,56,61,62,63,64,65,66\}. \end{align*}\]

\[\begin{align*} P(A|B)&=\frac{P(A\cap B)}{P(B)}\\ &=\frac{P(\{66\})}{P(\{16,26,36,46,56,61,62,63,64,65,66\})}\\ &=1/11. \end{align*}\]

In den Medien werden manchmal bedingte Wahrscheinlichkeiten berichtet, ohne dass das explizit erwähnt wird. Oftmals sind die berichteten bedingten Wahrscheinlichkeiten gar nicht die, für die man sich eigentlich interessiert, weil die Bedingung und das Bedingte quasi falsch herum angeordnet sind. Man interessiert sich für \(P(A|B)\) , berichtet wird aber \(P(B|A)\) .

Es wird berichtet, dass 50 Prozent der Studierenden ein “akademisches Elternhaus” haben (die Zahlen in diesem Beispiel sind fiktiv). Es handelt sich um die bedingte Wahrscheinlichkeit eines akademischen Elternhauses, wenn eine Person studiert. Hier sind die Ereignisse \(A\) : “Kind studiert”, und \(B\) : “akademisches Elternhaus”. Gegeben ist \(P(B|A)=0.5\) . Für die Bewertung der Chancengleichheit ist jedoch die bedingte Wahrscheinlichkeit interessanter, dass ein Kind studiert, wenn es aus einem akademischen Elternhaus stammt, also \(P(A|B)\) - und zwar im Vergleich zu der bedingten Wahrscheinlichkeit, dass ein Kind studiert, das nicht aus einem akademischen Elternhaus stammt, also \(P(A|\bar B)\) .

Wie kann man eine bedingte Wahrscheinlichkeit “umdrehen”? Wie verhält sich \(P(B|A)\) zu \(P(A|B)?\) Das sehen wir in Kürze im Kapitel 3.5 .

Bedingte Wahrscheinlichkeiten sind auch nützlich, um die Wahrscheinlichkeit zu berechnen, dass mehrere Ereignisse gemeinsam passieren. Dazu formen wir die Definition der bedingten Wahrscheinlichkeit einfach um. Aus \[ P(A|B)=\frac{P(A\cap B)}{P(B)} \] wird \[ P(A\cap B)={P(B)P(A|B)}. \] Das lässt sich auf mehr als zwei Ereignisse erweitern:

\[\begin{align*} P(A\cap B \cap C)&=P(C)P(B|C)P(A|B\cap C)\\ P(A\cap B\cap C\cap D)&=P(D)P(C|D)P(B|C\cap D)P(A|B\cap C\cap D) \end{align*}\]

Diese Formeln sind bei näherer Betrachtung intuitiv: Die Wahrscheinlichkeit, dass \(A\) , \(B\) und \(C\) gemeinsam eintreten, ergibt sich, indem man zuerst eine der unbedingten Wahrscheinlichkeiten nimmt (z.B. \(P(C)\) ). Nun ist \(C\) quasi eingetreten und wir arbeiten unter der Bedingung \(C\) weiter. Die Wahrscheinlichkeit \(P(C)\) wird jetzt mit der bedingten Wahrscheinlichkeit des nächsten Ereignisses multipliziert, also \(P(B|C)\) . Nun sind \(B\) und \(C\) eingetreten, und auf der nächsten Stufe multiplizieren wir deshalb mit \(P(A|B\cap C)\) . Eine andere Reihenfolge der Bedingungen wäre natürlich ebenfalls möglich, z.B. \[ P(A\cap B\cap C)=P(A)P(B|A)P(C|A\cap B). \] Für jede Reihenfolge gelangt man zum gleichen Ergebnis.

\[\begin{align*} P(A_5)&=P(A_5|A_4)P(A_4|A_3)P(A_3|A_2)P(A_2|A_1)P(A_1|A_0)\\ &=(1-k_{4,5})(1-k_{3,4})(1-k_{2,3})(1-k_{1,2})(1-k_{0,1}). \end{align*}\]

3.4 Totale Wahrscheinlichkeit

Aus mehreren bedingten Wahrscheinlichkeiten lässt sich eine unbedingte Wahrscheinlichkeit errechnen. Dazu zerlegen wir den Ergebnisraum \(\Omega\) in eine Partition. Unter einer Partition versteht man eine Zerlegung in disjunkte Mengen \(A_1, A_2, \ldots, A_n\) , so dass die Vereinigungsmenge der \(A_1,\ldots, A_n\) wieder \(\Omega\) ergibt. Die “Partitionierung eines Rinds” könnte etwa so aussehen:

Das Rind wird also vollständig in Teilmengen aufgeteilt, und alle Teilmengen zusammen ergeben wieder das gesamte Rind.

Sei \(A_1,\ldots,A_n\) eine Partition des Ergebnisraums \(\Omega\) . Für jedes Ereignis \(A_i\) , \(i=1,\ldots,n\) , sei die bedingte Wahrscheinlichkeit \(P(B|A_i)\) gegeben, wobei \(B\) irgendein Ereignis ist. Dann gilt für die unbedingte (totale) Wahrscheinlichkeit von \(B\) : \[ P(B)=\sum_{i=1}^n P(B|A_i)P(A_i). \]

Zur Begründung: Da \(A_1, A_2, \ldots, A_n\) eine Partition ist, gilt

\[\begin{align*} P(B) &= P((B\cap A_1)\cup (B\cap A_2)\cup\ldots\cup(B\cap A_n))\\ &= P(B\cap A_1)+P(B\cap A_2)+\ldots+P(B\cap A_n)\\ &= P(B|A_1)P(A_1)+P(B|A_2)P(A_2)+\ldots+P(B|A_n)P(A_n). \end{align*}\]

Eine besonders simple Partition ist die Unterteilung in \(A\) und \(\bar A\) . Dann lautet die Formel \[ P(B)=P(B|A)P(A)+P(B|\bar A)P(\bar A). \]

Die unbedingte Wahrscheinlichkeit ergibt sich als gewichtete Summe aller bedingten Wahrscheinlichkeiten, die Gewichtung erfolgt durch die Wahrscheinlichkeiten der bedingenden Ereignisse. Dieser Zusammenhang ist dann besonders nützlich, wenn die bedingten Wahrscheinlichkeiten schon bekannt oder einfach zu ermitteln sind, die unbedingte Wahrscheinlichkeit jedoch schwierig zu finden ist.

Eine Bank vergibt einen Kredit an ein Unternehmen. Das Unternehmen zahlt den Kredit mit einer Wahrscheinlichkeit von 0.95 zurück, wenn die konjunkturelle Lage positiv ist. Bei einer schwachen Konjunktur wird der Kredit jedoch nur mit einer Wahrscheinlichkeit von 0.8 zurückgezahlt. Die Wahrscheinlichkeit einer guten Konjunktur sei 0.75 (und die Konjunktur kann nur gut oder schlecht sein).

Als Ereignisse definiert man \(A\) : “gute Konjunktur” und \(B\) : “Kredit wird zurückgezahlt”. Gegeben sind die bedingten Wahrscheinlichkeiten \(P(B|A)=0.95\) und \(P(B|\bar A)=0.8\) . Außerdem ist \(P(A)=0.75\) bekannt. Damit ergibt sich die Wahrscheinlichkeit einer Rückzahlung als

\[\begin{align*} P(B)&=P(B|A)P(A)+P(B|\bar A)P(\bar A)\\ &=0.95\cdot 0.75+0.8\cdot 0.25\\ &=0.9125 \end{align*}\]

3.5 Satz von Bayes

Der Satz von Bayes setzt die beiden bedingten Wahrscheinlichkeiten \(P(A|B)\) und \(P(B|A)\) zueinander in Beziehung.

Für zwei Ereignisse \(A\) und \(B\) mit \(P(B)>0\) gilt der Satz von Bayes (engl. Bayes theorem) \[ P(A|B)=\frac{P(B|A)P(A)}{P(B)}. \]

Um die Bedingung und das Bedingte zu vertauschen, braucht man also die beiden unbedingten Wahrscheinlichkeiten. Die Herleitung des Satzes von Bayes ergibt sich aus der Definition der bedingten Wahrscheinlichkeit. Wegen

\[\begin{align*} P(A|B) &= \frac{P(A\cap B)}{P(B)}\\ P(B|A) &= \frac{P(A\cap B)}{P(A)} \end{align*}\]

gilt \[ P(A|B)P(B)=P(B|A)P(A). \] Daraus folgt durch Umstellen unmittelbar der Satz von Bayes.

Wir betrachten wieder den medizinischen Schnelltest und die beiden Ereignisse \(A\) : “Person ist infiziert”, und \(B\) : “Test positiv”. Neben den beiden bedingten Wahrscheinlichkeiten \(P(B|A)=0.99\) und \(P(\bar B|\bar A)=0.99\) sei bekannt, dass \(P(A)=0.001\) , d.h. nur mit einer Wahrscheinlichkeit von 0.1 Prozent ist eine zufällig aus der Population ausgewählte Person infiziert.

Wie groß ist Wahrscheinlichkeit, dass eine Person infiziert ist, bei der der Schnelltest ein positives Ergebnis zeigt? Gesucht ist also \(P(A|B)\) . Nach dem Satz von Bayes gilt \[ P(A|B)=\frac{P(B|A)P(A)}{P(B)}. \] Nach dem Satz der totalen Wahrscheinlichkeit berechnet man

\[\begin{align*} P(B) &=P(B|A)P(A)+P(B|\bar A)P(\bar A)\\ &= P(B|A)P(A)+[1-P(\bar B|\bar A)][1-P(A)]\\ &= 0.99\cdot 0.001+[1-0.99]\cdot [1-0.001]\\ &= 0.01098. \end{align*}\]

Dieser Wert kann nun zusammen mit \(P(A)\) und \(P(B|A)\) in die Bayes-Formel eingesetzt werden. Man erhält

\[\begin{align*} P(A|B) & = \frac{P(B|A)P(A)}{P(B)}\\ & = \frac{0.99 \times 0.001}{0.01098}\\ &\approx 0.0902. \end{align*}\]

Die Wahrscheinlichkeit, dass eine Person mit einem positiven Testergebnis tatsächlich infiziert ist, ist mit rund 9 Prozent folglich immer noch recht klein, obwohl der Test scheinbar sehr genau arbeitet.

3.6 Unabhängigkeit

Zwei Ereignisse \(A\) und \(B\) heißen unabhängig (oder auch stochastisch unabhängig , engl. independent bzw. stochastically independent), wenn \[ P(A\cap B)=P(A)\cdot P(B). \]

Eine alternative (fast äquivalente) Definition der Unabhängigkeit lautet so: Die Ereignisse \(A\) und \(B\) heißen unabhängig, wenn gilt \[ P(A|B)=P(A) \] bzw. wenn \[ P(B|A)=P(B). \] Die Definition über die bedingten Wahrscheinlichkeiten ist etwas intuitiver. Wenn das Wissen darüber, ob \(A\) eingetreten ist oder nicht, für die Wahrscheinlichkeit von \(B\) keine Rolle spielt (und umgekehrt), dann sind \(A\) und \(B\) unabhängig.

Achten Sie darauf, Unabhängigkeit nicht mit Disjunktheit zu verwechseln. Zur Erinnerung: Die Ereignisse \(A\) und \(B\) sind disjunkt, wenn \(A\cap B=\emptyset\) , so dass \(P(A\cap B)=0\) . Disjunkte Ereignisse können also nicht beide zusammen eintreten. Wenn \(A\) eintritt, kann man sicher sein, dass \(B\) nicht eintritt. Und wenn \(B\) eintritt, kann man sicher sein, dass \(A\) nicht eintritt. Unabhängige Ereignisse können hingegen sehr wohl zusammen eintreten.

Wir betrachten wieder den medizinischen Schnelltest und die beiden Ereignisse \(A\) : “Person ist infiziert”, und \(B\) : “Test positiv”. Zur Erinnerung: Gegeben sind die beiden bedingten Wahrscheinlichkeiten \(P(B|A)=0.99\) und \(P(\bar B|\bar A)=0.99\) sowie die unbedingte Wahrscheinlichkeit \(P(A)=0.001\) . Außerdem haben wir im letzten Abschnitt \(P(B)=0.01098\) berechnet.

Sind die Ereignisse \(A\) und \(B\) unabhängig? Die Antwort lautet “nein”, denn es gilt \[ 0.99=P(B|A)\neq P(B)=0.01098. \] Unabhängigkeit ist in diesem Fall natürlich auch nicht zu erwarten. Ein Schnelltest, dessen Ergebnis keinen Einfluss auf die Einschätzung der Wahrscheinlichkeit einer Infektion hätte, wäre vollkommen nutzlos.

• Report an issue

Laplace probability

Experiments in which all results are equally likely are called Laplace experiments .

The probability of an event is calculated in a Laplace experiment with the formula:

$|E| ...$ Number of results where $E$ occurs $|\Omega| ...$ Total number of results

Examples of Laplace experiments are the throwing of a coin, a dice or the turning of a wheel of fortune with fields of equal size.

A dice is thrown. Your are interested in the probability of an even number.

Sample space : $\Omega=\{1,2,3,4,5,6\}$ Event : $E=\{2, 4, 6\}$ Probability: $P(E) = \frac{|E|}{|\Omega|}$ $=\frac{3}{6}$

Non-Laplace experiment

In non-Laplace experiments , the probabilities for each possible outcome can not be determined by e.g. symmetry considerations or the like. However, after many experiments have been carried out, estimates of the probabilities can be determined.

Examples of non-Laplace experiments are the throwing of thumbtacks, a LEGO stone or a crown cork. It is not exactly possible to say which event occurs with which probability.