black hole theory research paper

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Black holes

• Author information
• Copyright and License information

To whom reprint requests should be addressed. E-mail: [email protected] .

Recent progress in black hole research is illustrated by three examples. We discuss the observational challenges that were met to show that a supermassive black hole exists at the center of our galaxy. Stellar-size black holes have been studied in x-ray binaries and microquasars. Finally, numerical simulations have become possible for the merger of black hole binaries.

Black holes are a striking example of a prediction of Einstein's theory of gravity, general relativity. Although it took many decades before the physical concept of a black hole was fully understood and widely accepted, recent years have seen rapid advances on both the observational and theoretical side, which we want to illustrate in this brief note with three examples. Black holes have become an astrophysical reality. Solid observational evidence exists for black holes in two mass ranges. Supermassive black holes of 10 6 -10 9 solar masses have been observed at the centers of many galaxies, and here we discuss the observational challenges that were met to show that there exists a black hole at the center of our own galaxy. Stellar-size black holes of about 3–20 solar masses have been studied in x-ray binaries and microquasars. Finally, numerical simulations have become possible for the merger of black hole binaries.

The Galaxy's Central Supermassive Black Hole.

Recent high-resolution imaging studies of stars at the center of our Galaxy have produced strong dynamical evidence for a central concentration of dark matter, establishing the Milky Way as the most convincing case of a galaxy containing a central supermassive black hole ( 1 , 2 ). In those experiments, images obtained over 2–6 years at the Keck telescope ( 1 ) and European Southern Observatory's New Technology Telescope ( 2 ) provided measurements of the stars' velocities in the plane of the sky, from which a statistical analysis revealed the existence of 2−3 × 10 6 solar masses of dark matter contained within a radius of 0.015 parsec (1 parsec = 3.09 × 10 16 m), or 2.6 light weeks. At this meeting, new results from the Keck telescope were reported. With this new data set, which triples the number of maps obtained and doubles the time baseline for the Keck experiment, the velocity uncertainties are reduced by a factor of 3 compared with the earlier Keck work ( 1 ), primarily as a result of the increased time baseline and, in the central square arcsecond, by a factor of 6 compared with ref. 2 , due to the higher angular resolution (0."05 vs. 0."15). In addition to simply increasing the time baseline for velocity measurements, the new measurements have advanced this experiment in two significant ways: ( i ) the first Keck adaptive optics (AO) images of the galactic center have been obtained (Fig. 1 ), allowing a more complete census of stars in this region to be obtained ( 3 ), and ( ii ) the first measurements of stellar accelerations in this field have now been achieved ( 4 ).

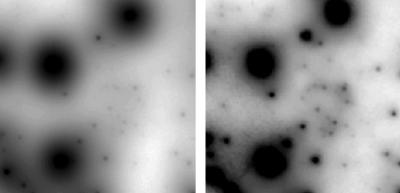
A ≈3" × 3" region showing the Sgr A* cluster (the faint stars located just to the right of the center of the field of view). Both images were taken in May 1999 at 2.2 μm (K-band); however, the image on the left was produced by shift-and-adding Keck I speckle data, and the image on the right was obtained with the new Keck II adaptive optics system. The adaptive optics image represents a large improvement.

With longer integration times, AO should probe a yet larger sample of fainter stars, place stringent limits on Sgr A*, and explore the possibility of a gravitational lensing experiment ( 5 ). For the time being, the AO map has increased the number of stars in the proper motion study ( 3 ). With relative positional accuracies of ≈3 milliarcseconds, the motions of stars are now fit with a second-order polynomial as opposed to a simple linear fit, which was done in earlier work. Among the 90 stars in the original Keck proper motion sample ( 1 ), accelerations of 2–5 milliarseconds/yr 2 , or equivalently 3–6 × 10 −6 km/sec 2 , are now detected for three stars, S0–1, S0–2, and S0–4 ( 4 ). These three stars are independently distinguished in this sample as being among the fastest moving stars ( v = 565 to 1,383 km/sec) and among the closest to the nominal position of Sgr A* (< r > = 0.003 to 0.015 parsec). Acceleration vectors, in principle, are more precise tools than velocity vectors for studying the properties of the central dark mass. These acceleration measurements improve the localization of our Galaxy's dynamical center by a factor of 3, which is critical for reliably associating any near-infrared source with the black hole, given the complexity of the region. In addition, these acceleration measurements increase the minimum mass density inferred by a factor of 8 over previous results, thereby strengthening the case for a black hole.

X-Ray Binaries and Microquasars.

In contrast to the need for measuring dozens of stars to determine the mass of the black hole in the Galactic Center, that of black holes in x-ray binary systems can be deduced either from optical/IR measurements of just one star, namely the companion of the stellar-mass black hole, or from x-ray observations of the binary. In x-ray binaries, a black hole of typically 3–10 solar masses and a normal star (1–30 solar masses) orbit each other. Matter is pulled off the companion star and, because of its angular momentum, is forming an accretion disk as it moves toward the black hole. Before finally falling into the black hole, the matter heats up to several million degrees at the inner part of the disk and emits luminous x-ray radiation. Because the whole accretion process is highly variable, numerous such black hole binaries have been found over the last decade, thanks to x-ray detectors on satellites, such as Compton Gamma-Ray Observatory and Rossi X-Ray Timing Explorer, constantly monitoring the whole sky.

Although optical/IR spectroscopic measurements of the velocity of the companion star can readily determine the mass of the black hole, x-ray measurements promise to be a sharper and even more flexible diagnostic tool as they reach down to the inner edge of the accretion disk at a few Schwarzschild radii of the black hole. High time-resolution observations of black hole binaries have revealed quasiperiodic oscillations in x-ray emission at a stable minimum period, e.g., at 67 Hz for GRS 1915 + 105 ( 6 ), which may very well be related to the period of the innermost stable orbit of the accretion disk. The Kerr metric fixes this period as a function of mass and spin of the black hole. Because the maximum temperature of the innermost disk, as discernable from x-ray spectroscopy, is also thought to be just a function of black hole mass and spin, detailed x-ray observations can be used to determine both the mass AND spin of a black hole ( 7 ).

A small fraction of black hole binaries also eject matter at relativistic speeds into two opposite jets that are observable in the radio band as knots moving apart at superluminal speed. Actually, GRS 1915 + 105 is the most famous representative of this class of object, called microquasars ( 8 ). Simultaneous observations of these microquasars in the x-ray, optical/IR, and radio band have for the first time revealed a relation between accretion disk instabilities and jet ejections ( 9 , 10 ). Theorists now face the challenge of modeling the highly dynamical processes of nonsteady accretion and jet formation, acceleration, and collimation, with all of the complications of three-dimensional magnetohydrodynamics and general relativity.

Numerical Simulations.

Another example in which the full Einstein equations have to be solved in the highly dynamic and nonlinear regime is the collision and merger of two black holes. In fact, although single black holes are comparatively simple exact solutions of the Einstein equations, the two-body problem of general relativity for black holes, or neutron stars, is unsolved. As opposed to Newtonian theory, where the Kepler ellipses provide an astrophysically relevant example for the analytic solution of the two-body problem, in Einsteinian gravity there are no corresponding exact solutions. The failure of Einstein's theory to lead to stable orbits is due to the fact that, in general, two orbiting bodies will emit gravitational waves that carry away energy and momentum from the system, leading to an inspiral. Of course, this “leak” is not considered detrimental. It is expected that gravitational wave astronomy will open a new window onto the universe ( 11 ), and binary black hole mergers are considered to be among the most likely candidates for first detection.

Numerical relativity is only now approaching a state where the evolution of rather general three-dimensional data sets can be simulated on a computer to solve the Einstein equations (see, e.g., ref. 12 ). After early computations for the axisymmetric head-on collision of two black holes in the 1970s, it was in 1995 that, for the first time, spherically symmetric data for a single Schwarzschild black hole was evolved with a three-dimensional computer code ( 13 ). The first fully three-dimensional binary black hole evolutions, the grazing collision of nearby spinning and moving black holes, is reported in ref. 14 . Fig. 2 shows a visualization of such a black hole merger [M. Alcubierre, W. Benger, B. Brügmann, G. Lanfermann, L. Nerger, E. Seidel & R. Takahashi, R. http://jean-luc.aei.mpg.de/Press/BH1999/ ]. These simulations are still severely limited in achievable evolution time (300 μs for a final black hole of 10 solar masses), i.e., one can evolve through the very last moments of the inspiral when the two black holes merge, but even a single full orbit is not yet possible. Concretely, the computer code crashes when the space–time distortion becomes too severe. The recent computer simulations not only reflect an increase in raw computer power but also are due to theoretical work on how to construct good coordinates dynamically to deal with strong and even singular gravitational fields, and a new way to compute black hole initial data was developed. Work is in progress to obtain at least one orbit and to compute the gravitational waves generated in a black hole merger.

The evolution of the apparent horizon during a grazing black hole collision. Initially there are two separate horizons, which, during the merger, become enclosed by a third one. The coloring represents the curvature of the surface. The black holes appear to grow, because numerical grid points are falling toward and into the black hole.

In conclusion, we believe that black hole physics will be a very dynamic field in the coming years.

Acknowledgments

A.M.G. was supported by the National Science Foundation and the Packard Foundation. J.G. was partly supported by the German Bundesministerium für Bildung, Wissenschaft, Forschung und Technologie (BMBF/DLR) under contract 50 QQ 9602 3. The simulations in refs. 14 and 15 were performed at the Albert-Einstein-Institut and at National Center for Supercomputing Applications.

This paper is a summary of a session presented at the sixth annual German–American Frontiers of Science symposium, held June 8–10, 2000, at the Arnold and Mabel Beckman Center of the National Academies of Science and Engineering in Irvine, CA.

• 1. Ghez A M, Klein B L, Morris M, Becklin E E. Astrophys J. 1998;509:678–686. [ Google Scholar ]
• 2. Genzel R, Pichon C, Eckart A, Gerhard O E, Ott T. Mon Not R Astron Soc. 2000;317:348–374. [ Google Scholar ]
• 3. Wizinowich P, Acton D S, Shelton C, Stomski P, Gathright K, Ho W, Lupton W, Tsubota K, Lai O, Max C, et al. PASP. 2000;112:315–319. [ Google Scholar ]
• 4. Ghez A M, Morris M, Becklin E E, Tanner A, Kremenek T. Nature (London) 2000;407:349–351. doi: 10.1038/35030032. [ DOI ] [ PubMed ] [ Google Scholar ]
• 5. Alexander T, Sternberg A. Astrophys J. 1999;520:137–148. [ Google Scholar ]
• 6. Morgan E H, Remillard R A, Greiner J. Astrophys J. 1997;482:993–1010. [ Google Scholar ]
• 7. Zhang N S, Cui W, Chen W. Astrophys J. 1997;482:L155–L158. [ Google Scholar ]
• 8. Greiner J. In: Cosmic Explosions, Proc. 10th Ann. Astrophys. Conf. in Maryland. Holt S, Zhang W W, editors. Vol. 522. Melville, NY: American Institute of Physics; 2000. pp. 307–316. [ Google Scholar ]
• 9. Greiner J, Morgan E H, Remillard R A. Astrophys J. 1996;473:L107–L110. [ Google Scholar ]
• 10. Mirabel I F, Dhawan V, Chaty S, Rodriguez L F, Marti J, Robinson C R, Swank J, Geballe T R. Astron Astrophys. 1998;330:L9–L12. [ Google Scholar ]
• 11. Schutz B. Class Quant Grav. 1999;16:A131–A156. [ Google Scholar ]
• 12. Brügmann B. Ann Phys (Leipzig) 2000;9:227. [ Google Scholar ]
• 13. Anninos P, Camarda K, Massó J, Seidel E, Suen W-M, Towns J. Phys Rev D. 1995;52:2059–2082. doi: 10.1103/physrevd.52.2059. [ DOI ] [ PubMed ] [ Google Scholar ]
• 14. Brügmann B. Int J Mod Phys D. 1999;8:85–100. [ Google Scholar ]
• View on publisher site
• PDF (135.8 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections